题目内容
17.已知数列{an}满足a1=1,且${a_{n+1}}=\frac{a_n}{{1+{a_n}}}$(n=1,2,3,…,)(Ⅰ)求a2,a3,a4的值,并猜想出这个数列的通项公式;
(Ⅱ)求S=a1a2+a2a3+a3a4+…+a7a8的值.
分析 (Ⅰ)由代入法,计算数列的前4项,猜想an=$\frac{1}{n}$(n∈N*),可由数学归纳法证明;
(Ⅱ)由anan+1=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用裂项相消求和,即可得到所求和.
解答 解:(Ⅰ)∵a1=1,∴${a_2}=\frac{a_1}{{1+{a_1}}}=\frac{1}{2},{a_3}=\frac{a_2}{{1+{a_2}}}=\frac{1}{3},{a_4}=\frac{1}{4}$,
猜想${a_n}=\frac{1}{n},(n∈{N^*})$.
理由:当n=1时,a1=1显然成立;
设n=k(k∈N*)ak=$\frac{1}{k}$,
当n=k+1时,ak+1=$\frac{{a}_{k}}{1+{a}_{k}}$=$\frac{\frac{1}{k}}{1+\frac{1}{k}}$=$\frac{1}{1+k}$,
则n=k+1,猜想也成立.
则an=$\frac{1}{n}$(n∈N*);
(Ⅱ)S=a1a2+a2a3+a3a4+…+a7a8,
即有$S=\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{7×8}$=$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{7}-\frac{1}{8})=1-\frac{1}{8}=\frac{7}{8}$.
点评 本题考查数列的通项公式,注意运用猜想和证明,考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
7.某土特产销售总公司为了解其经营状况,调查了其下属各分公司月销售额和利润,得到数据如下表:
在统计中发现月销售额x和月利润额y具有线性相关关系.
(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;
(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overrightarrow{x}•\overrightarrow{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overrightarrow{x}}^{2}}$,$\widehat{a}$=$\overrightarrow{y}$-$\widehat{b}$$\overrightarrow{x}$,其中:$\sum_{i=1}^{n}{x}_{i}{y}_{i}$=112,$\sum_{i=1}^{n}{x}_{i}^{2}$=200).
| 分公司名称 | 雅雨 | 雅雨 | 雅女 | 雅竹 | 雅茶 |
| 月销售额x(万元) | 3 | 5 | 6 | 7 | 9 |
| 月利润y(万元) | 2 | 3 | 3 | 4 | 5 |
(Ⅰ)根据如下的参考公式与参考数据,求月利润y与月销售额x之间的线性回归方程;
(Ⅱ)若该总公司还有一个分公司“雅果”月销售额为10万元,试求估计它的月利润额是多少?(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overrightarrow{x}•\overrightarrow{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overrightarrow{x}}^{2}}$,$\widehat{a}$=$\overrightarrow{y}$-$\widehat{b}$$\overrightarrow{x}$,其中:$\sum_{i=1}^{n}{x}_{i}{y}_{i}$=112,$\sum_{i=1}^{n}{x}_{i}^{2}$=200).
8.椭圆x2+my2=1的长轴长为4,则其焦点坐标为( )
| A. | (±3,0) | B. | (±1,0) | C. | (0,±1) | D. | (0,±$\sqrt{3}$) |
5. 为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
的频率之比为1:2:3,第1小组的频数为6,则报考飞行员的学生人数是( )
 为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组
为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第1小组的频数为6,则报考飞行员的学生人数是( )
| A. | 32 | B. | 40 | C. | 48 | D. | 56 |
12.如果a<b<0,c>d>0,那么一定有( )
| A. | $\frac{c}{a}>\frac{d}{b}$ | B. | $\frac{c}{a}<\frac{d}{b}$ | C. | $\frac{c}{b}>\frac{d}{a}$ | D. | $\frac{c}{b}<\frac{d}{a}$ |
2.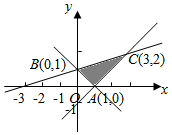 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
 设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )
设x,y满足如图所示的可行域(阴影部分),则$z=\frac{1}{2}x-y$的最大值为( )| A. | $\frac{1}{2}$ | B. | 0 | C. | $-\frac{1}{2}$ | D. | -1 |