题目内容
19．函数f（x）=$\sqrt{lg（5-{x}^{2}）}$的定义域是[-2，2]．分析 由根式内部的代数式大于等于0求解对数不等式得答案．
解答 解：由lg（5-x2）≥0，得5-x2≥1，
即x2≤4，解得-2≤x≤2．
∴函数f（x）=$\sqrt{lg（5-{x}^{2}）}$的定义域是[-2，2]．
故答案为：[-2，2]．
点评 本题考查函数的定义域及其求法，是基础的计算题．
练习册系列答案
相关题目
10．已知函数$f（x）=lnx+ax-\frac{1}{x}+b$．
（1）若函数$g（x）=f（x）+\frac{2}{x}$为减函数，求a的取值范围；
（2）若f（x）≤0恒成立，证明：a≤1-b．
（1）若函数$g（x）=f（x）+\frac{2}{x}$为减函数，求a的取值范围；
（2）若f（x）≤0恒成立，证明：a≤1-b．
7．设双曲线$\frac{{x}^{2}}{3}$-y2=1的两焦点分别为F1，F2，P为双曲线上的一点，若PF1与双曲线的一条渐近线平行，则cos∠F1PF2=（ ）
| A． | $-\frac{11}{13}$ | B． | $-\frac{11}{12}$ | C． | $-\frac{7}{12}$ | D． | $-\frac{1}{13}$ |
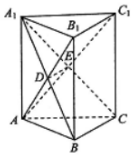如图，在直三棱柱ABC-A1B1C1中，AC⊥BC，A1B与AB1交于点D，A1C与AC1交于点E．
11．设f（x）是定义在R上的奇函数，当x≤0时，f（x）=2x2-x，则f（1）=（ ）
| A． | 1 | B． | 3 | C． | -3 | D． | 0 |
如图，在△ABC中，AB=BC=$\sqrt{6}$，∠ABC=90°，点D为AC的中点，将△ABD沿BD折起到△PBD的位置，使PC=PD，连接PC，得到三棱锥P-BCD，若该三棱锥的所有顶点都在同一球面上，则该球的表面积是（ ）