题目内容
已知an=n2+n,bn=(-1)n-1,(n∈N*),设cn=
,数列{cn}的前n项和为Tn,求证:T2n<1.
| (2n+1)bn |
| an |
考点:数列的求和
专题:等差数列与等比数列
分析:由cn=(-1)n-1•
,得到c2n-1+c2n=
-
,由此利用裂项求和法能证明T2n<1.
| 2n+1 |
| n(n+1) |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
证明:an=n2+n,bn=(-1)n-1,(n∈N*),
∴cn=
=(-1)n-1•
,
∴c2n-1+c2n=
-
=
=
=
-
,
∴T2n═(c1+c2)+(c3+c4)+…+(c2n-1+c2n)
=1-
+
-
+…+
-
=1-
<1.
∴T2n<1.
∴cn=
| (2n+1)bn |
| an |
| 2n+1 |
| n(n+1) |
∴c2n-1+c2n=
| 4n-1 |
| 2n(2n-1) |
| 4n+1 |
| 2n(2n+1) |
=
| (4n-1)(2n+1)-(4n+1)(2n-1) |
| 2n(2n-1)(2n+1) |
=
| 2 |
| (2n-1)(2n+1) |
=
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴T2n═(c1+c2)+(c3+c4)+…+(c2n-1+c2n)
=1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=1-
| 1 |
| 2n+1 |
∴T2n<1.
点评:本题考查考查不等式的证明,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数
等于( )
| i3 |
| 1-i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|

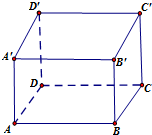 用长为18的钢条围成一个长方体形状的框架,设长方体的宽为x,长为2x,其体积为y
用长为18的钢条围成一个长方体形状的框架,设长方体的宽为x,长为2x,其体积为y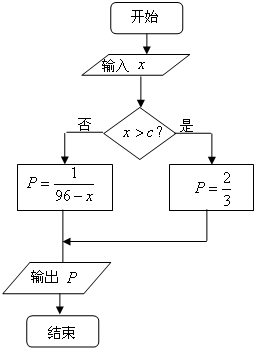 某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=
某厂生产一种仪器,由于受生产能力与技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率p与日产量x(件)(x∈N*)之间大体满足如框图所示的关系(注:次品率P=