题目内容
圆锥的侧面展开图是半径为2的扇形，其面积是2π，则该圆锥的体积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由题意和侧面展开图的面积．求出圆锥底面的半径以及高，再求出圆锥的体积即可．
解答：
解：设圆锥的底面半径为r，高为h，
因为圆锥的侧面展开图是半径为2的扇形，其面积是2π，
所以πr×2=2π，解得r=1，则h=
=
，
所以该圆锥的体积V=
×π×
=
，
故答案为：
．
因为圆锥的侧面展开图是半径为2的扇形，其面积是2π，
所以πr×2=2π，解得r=1，则h=
| 22-1 |
| 3 |
所以该圆锥的体积V=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查旋转体：圆锥的体积，以及侧面展开图的应用，考查空间想象能力，计算能力．
练习册系列答案
相关题目
已知正四面体ABCD中，棱长为a，M、N分别为BC、AD的中点．求：设F1、F2为椭圆C：
+
=1（a＞b＞0）的左、右焦点，直线l过焦点F2且与椭圆交于A，B两点，若△ABF1构成以A为直角顶点的等腰直角三角形，设椭圆离心率为e，则e2=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、2-
| ||
B、3-
| ||
C、11-6
| ||
D、9-6
|
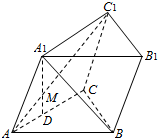如图，已知斜三棱柱ABC-A1B1C1中，∠BCA=90°，AC=BC=a，点A1在底面ABC上的射影恰为AC的中点D，A1D∩AC1=M，BA1⊥AC1．