题目内容
4.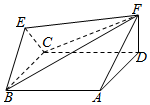 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.(Ⅰ)求证:EF∥平面ABCD;
(Ⅱ)若∠CBA=60°,求几何体EFABCD的体积.
分析 (Ⅰ)根据线面平行的判定定理即可证明EF∥平面ABCD;
(Ⅱ)若∠CBA=60°,利用分割法结合棱锥和棱柱的体积公式即可求几何体EFABCD的体积.
解答  解:(Ⅰ)如图,过点E作EH⊥BC于H,连接HD.
解:(Ⅰ)如图,过点E作EH⊥BC于H,连接HD.
∴$EH=\sqrt{3}$.
∵平面ABCD⊥平面BCE,EH⊆平面BCE,
平面ABCD∩平面BCE于BC,
∴EH⊥平面ABCD.
又∵FD⊥平面ABCD,$FD=\sqrt{3}$.
∴$FD\underline{\underline{∥}}EH$.
∴四边形EHDF为平行四边形.
∴EF∥HD.
∵EF?平面ABCD,HD⊆平面ABCD,
∴EF∥平面ABCD.…(6分)
(Ⅱ)连接CF,HA.由题意,得HA⊥BC.
∵HA⊆平面ABCD,平面ABCD⊥平面BCE于BC,
∴HA⊥平面BCE.
∵FD∥EH,EH⊆平面BCE,FD?平面BCE,
∴FD∥平面BCE.
同理,由HB∥DA可证,DA∥平面BCE.
∵FD∩DA于D,FD?平面ADF,DA?平面ADF,
∴平面BCE∥平面ADF.
∴F到平面BCE的距离等于HA的长.
∵FD为四棱锥F-ABCD的高,
∴VEFABCD=VF-BCE+VF-ABCD=$\frac{1}{3}{S_{△BCE}}×HA+\frac{1}{3}{S_{平行四边形ABCD}}×FD$=$\frac{1}{3}×\sqrt{3}×\sqrt{3}+\frac{1}{3}×2\sqrt{3}×\sqrt{3}$=3.…(12分)
点评 本题主要考查空间几何体线面平行的判定以及几何体的体积的计算,利用相应的判定定理以及分割法是解决本题的关键.

练习册系列答案
相关题目
9.设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x,且一个焦点与抛物线x2=4y的焦点相同,则此双曲线的方程为( )
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |
16.设O为坐标原点,F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点,若在双曲线上存在点M,满足∠F1MF2=60°,|OM|=2a,则该双曲线的渐近线方程为( )
| A. | x±2y=0 | B. | 2x±y=0 | C. | x±y=0 | D. | $\sqrt{2}x±y=0$ |
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,且斜率为2的直线l与双曲线的相交于点A,B,若弦AB的中点横坐标取值范围为(2c,4c),则该双曲线的离心率的取值范围是( )
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |