题目内容
17.等差数列{an}中,若S20=170,则a7+a8+a10+a17=34.分析 根据等差数列的通项公式与前n项和公式,进行化简运算即可.
解答 解:等差数列{an}中,S20=170,
∴$\frac{{(a}_{1}{+a}_{20})×20}{2}$=170,
∴a1+a20=17,
即2a1+19d=17;
∴a7+a8+a10+a17=4a1+38d=2(2a1+19d)=34.
故答案为:34.
点评 本题考查了等差数列的通项公式与前n项和公式的应用问题,是基础题目.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
8.已知sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$,其中$\frac{π}{2}$<θ<π,则tanθ=( )
| A. | -$\sqrt{2}$ | B. | -$\frac{12}{5}$ | C. | -2 | D. | -$\frac{5}{12}$ |
8.已知椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1({a_1}>{b_1}>0)$与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1({a_2}>0,{b_2}>0)$有相同的焦点F1,F2,点P是两曲线的一个公共点,且PF1⊥PF2,e1,e2分别是两曲线C1,C2的离心率,当4e12+e22取得最小值时,C1的离心率e1等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
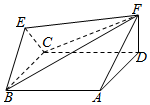 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.