题目内容
16.设O为坐标原点,F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的焦点,若在双曲线上存在点M,满足∠F1MF2=60°,|OM|=2a,则该双曲线的渐近线方程为( )| A. | x±2y=0 | B. | 2x±y=0 | C. | x±y=0 | D. | $\sqrt{2}x±y=0$ |
分析 设M为右支上一点,|F1M|=s,|MF2|=t,运用余弦定理和双曲线的定义、中线长公式,化简整理,解方程可得离心率和渐近线方程.
解答 解:在△F1MF2中,∠F1MF2=60°,|OM|=2a,
设M为右支上一点,|F1M|=s,|MF2|=t,
即有s2+t2-2stcos60°=4c2,①
又s-t=2a②,2(s2+t2)=4c2+16a2③
联立①②③可得c2=2a2,a=b,
即有e=$\frac{c}{a}$=$\sqrt{2}$,渐近线方程为y=±$\frac{b}{a}$x,即为y=±x.
故选:C.
点评 本题考查双曲线的定义、方程和性质,考查三角形中的余弦定理的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
4.M={x|5-x≥$\sqrt{2(x-1)}$},N={x|x2-ax≤x-a},当M?N时,a的取值范围是( )
| A. | a≥3 | B. | a≤3 | C. | a<3 | D. | a>3 |
8.已知椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1({a_1}>{b_1}>0)$与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1({a_2}>0,{b_2}>0)$有相同的焦点F1,F2,点P是两曲线的一个公共点,且PF1⊥PF2,e1,e2分别是两曲线C1,C2的离心率,当4e12+e22取得最小值时,C1的离心率e1等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
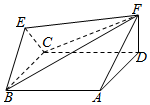 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.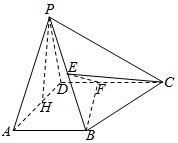 如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.
如图所示,在四棱锥P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中点,F是DC上的点且DF=$\frac{1}{2}$AB,PH为△PAD中AD边上的高.