题目内容
10.函数f(x)与g(x)=($\frac{1}{2}$)x的图象关于直线y=x对称,则f(x2-2x)的单增区间为( )| A. | (-∞,0) | B. | (2,+∞) | C. | (0,1) | D. | [1,2) |
分析 由条件可知f(x),g(x)互为反函数,从而得到$f(x)=lo{g}_{\frac{1}{2}}x$,这便得出$f({x}^{2}-2x)=lo{g}_{\frac{1}{2}}({x}^{2}-2x)$,该函数是由$y=lo{g}_{\frac{1}{2}}t$和t=x2-2x复合而成的复合函数,根据复合函数的单调性即可求出该函数的单调增区间.
解答 解:由题意知,f(x)与g(x)互为反函数;
∴$f(x)=lo{g}_{\frac{1}{2}}x$;
∴$f({x}^{2}-2x)=lo{g}_{\frac{1}{2}}({x}^{2}-2x)$,令x2-2x=t,t>0,则$y=lo{g}_{\frac{1}{2}}t$为减函数;
t=x2-2x的单调减区间为(-∞,0);
∴复合函数f(x2-2x)的单调增区间为(-∞,0).
故选:A.
点评 考查反函数的概念,反函数和原函数图象的对称性,以及指数式和对数式的互化,对数函数和二次函数的单调性,复合函数单调区间的求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.运行如图所示程序框图,输出的结果是( )


| A. | 15 | B. | 23 | C. | 47 | D. | 95 |
5.已知点F1,F2是椭圆C:$\frac{x^2}{4}+{y^2}$=1的焦点,点M在椭圆C上且满足|$\overrightarrow{M{F}_{1}}$+$\overrightarrow{M{F}_{2}}$|=2$\sqrt{3}$,则△MF1F2的面积为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
15.已知命题p:所有有理数都是实数;命题q:y=x2是奇函数.则下列命题中为真命题的是( )
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨(¬q) |
2.设f(x)为定义在R上的奇函数,当x>0时,f(x)=log2(x+7),则f(-1)=( )
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
19.函数f(x)=a3sina+5a2x2的导数f′(x)=( )
| A. | 3a2cosa+10ax2 | B. | 3a2cosa+10ax2+10a2x | ||
| C. | a3sina+10a2x | D. | 10a2x |
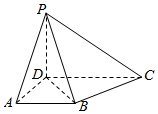 在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.