题目内容
7.若直线y=x+m与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1有两个公共点,则m的取值范围是( )| A. | (-5,5) | B. | (-2,2) | C. | (-$\sqrt{7}$,$\sqrt{7}$) | D. | (-$\sqrt{3}$,$\sqrt{3}$) |
分析 当直线与椭圆有公共点时,直线方程与椭圆方程构成的方程组有解,等价于消掉y后得到x的二次方程有解,故△>0,解出即可.
解答 解:由$\left\{\begin{array}{l}y=x+m\\ \frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1\end{array}\right.$,得7x2+8mx+4m2-12=0,
当直线与椭圆有公共点时,△=64m2-4×7(4m2-12)>0,即-3m2+21>0,
解得-$\sqrt{7}$<m<$\sqrt{7}$,
∴实数m的取值范围是,(-$\sqrt{7}$,$\sqrt{7}$).
故选:C.
点评 本题考查直线与圆锥曲线的位置关系,考查函数与方程思想,属于中档题.

练习册系列答案
相关题目
17.若4≤a≤8,0≤b≤2,则a+b的取值范围是( )
| A. | (4,10) | B. | [4,10] | C. | (6,8) | D. | [6,8] |
12.把函数f(x)=2sin(2x+$\frac{π}{6}$)的图象沿x轴向左平移$\frac{π}{6}$个长度单位,得到函数g(x)的图象,关于函数g(x),下列说法正确的是( )
| A. | 在[$\frac{π}{4}$,$\frac{π}{2}$]上是增函数 | |
| B. | 其图象关于直线x=-$\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当x∈[$\frac{π}{6}$,$\frac{2π}{3}$]时,函数g(x)的值域是[-2,1] |
16.某几何体的三视图如图所示,则该几何体的体积为( )
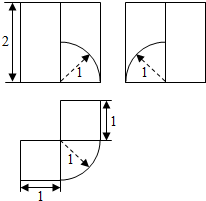

| A. | 6+$\frac{π}{8}$ | B. | 6+$\frac{π}{6}$ | C. | 4+$\frac{π}{8}$ | D. | 4+$\frac{π}{6}$ |
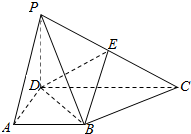 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=90°,AB=AD=PD=2,CD=4.