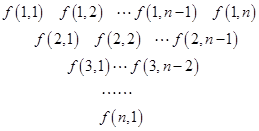题目内容
数列 的前
的前 项和记为
项和记为 ,已知
,已知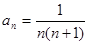 .
.
(Ⅰ)求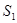 ,
, ,
,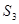 的值,猜想
的值,猜想 的表达式;
的表达式;
(Ⅱ)请用数学归纳法证明你的猜想.
(Ⅰ) ;(Ⅱ)假设当
;(Ⅱ)假设当 时,猜想成立,即
时,猜想成立,即 .那么当
.那么当 时,
时, ,
,
所以当 时,猜想成立.
时,猜想成立.
解析试题分析:(Ⅰ)根据题设条件,可求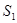 ,
, ,
,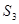 的值,猜想
的值,猜想 的表达式.(Ⅱ)利用数学归纳法的证明步骤对这个猜想加以证明.
的表达式.(Ⅱ)利用数学归纳法的证明步骤对这个猜想加以证明.
试题解析:(Ⅰ)因为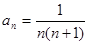 ,所以
,所以 ,
, ,
, .
.
所以猜想 ;(Ⅱ)证明:(1)当
;(Ⅱ)证明:(1)当 时,
时, ,猜想成立.
,猜想成立.
(2)假设当 时,猜想成立,即
时,猜想成立,即 .那么当
.那么当 时,
时, ,
,
所以当 时,猜想成立.
时,猜想成立.
考点:数学归纳法;数列递推式.

练习册系列答案
相关题目
 表示第
表示第 幅图的蜂巢总数.则
幅图的蜂巢总数.则 =______;
=______;
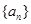 是公比为q的等比数列,其前n项的积为
是公比为q的等比数列,其前n项的积为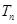 ,并且满足条件
,并且满足条件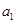 >1,
>1,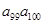 >1,
>1, 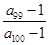 <0,给出下列结论:① 0<q<1;② T198<1;③
<0,给出下列结论:① 0<q<1;② T198<1;③ 满足
满足 ,则
,则 __________
__________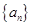 满足对任意的
满足对任意的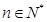 ,都有
,都有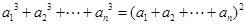 且
且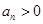 .
.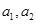 的值;
的值;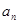 ;
;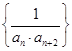 的前
的前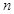 项和为
项和为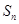 ,不等式
,不等式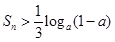 对任意的正整数
对任意的正整数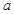 的取值范围.
的取值范围. 的前n项和为
的前n项和为 ,且
,且
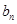 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
; 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。 的首项
的首项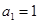 ,前
,前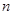 项和为
项和为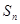 ,且
,且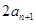 ,
,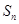 ,
,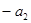 成等差数列,其中
成等差数列,其中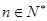 .
.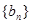 满足:
满足: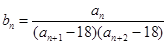 ,记数列
,记数列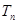 ,求
,求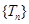 的最大项.
的最大项.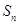 ,
,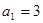 ,满足
,满足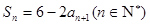 ,
,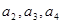 的值;
的值;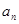 的表达式.
的表达式.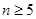 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: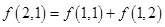 ;
;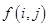 为数表中第
为数表中第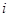 行的第
行的第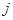 个数.
个数.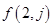 和
和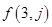 ;
;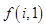 关于
关于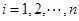 )的表达式.
)的表达式.