题目内容
一个三角形数表按如下方式构成(如图:其中项数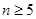 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: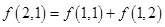 ;
;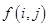 为数表中第
为数表中第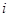 行的第
行的第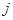 个数.
个数.
(1)求第2行和第3行的通项公式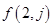 和
和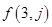 ;
;
(2)证明:数表中除最后2行外每一行的数都依次成等差数列;
(3)求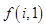 关于
关于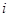 (
(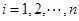 )的表达式.
)的表达式.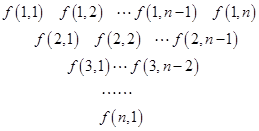
(1)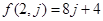 ,
, ;(2)证明见解析,
;(2)证明见解析,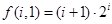 ;(3)
;(3) .
.
解析试题分析:(1)根据定义, ,因此
,因此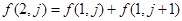
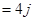
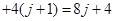 ,
,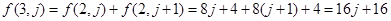 ;(2)由于第
;(2)由于第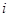 行的数依赖于第
行的数依赖于第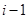 的数,因此我们可用数学归纳法证明;(3)设第
的数,因此我们可用数学归纳法证明;(3)设第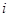 行的公差为
行的公差为 ,
,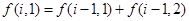
 ,而
,而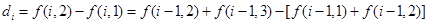
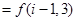
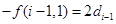 ,从而
,从而 ,即
,即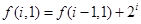 ,于是有
,于是有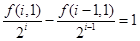 ,由此可求得数列
,由此可求得数列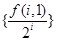 是公差为1的等差数列,而
是公差为1的等差数列,而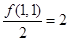 ,由等差数列通项公式得
,由等差数列通项公式得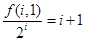 ,从而有
,从而有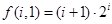 .
.
试题解析:(1)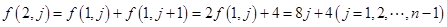
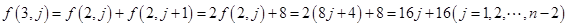 . (4分)
. (4分)
(2)由已知,第一行是等差数列,
假设第 行是以
行是以 为公差的等差数列,则由
为公差的等差数列,则由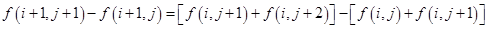
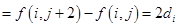 (常数)
(常数)
知第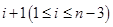 行的数也依次成等差数列,且其公差为
行的数也依次成等差数列,且其公差为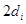 .
.
综上可得,数表中除最后2行以外每一行都成等差数列. (9分)
(3)由于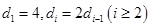 ,所以
,所以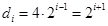 , (11分)
, (11分)
所以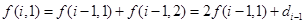 ,
,
由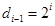 得
得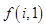
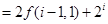 , (13分)
, (13分)
于是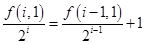 ,即
,即 , (15分)
, (15分)
又因为 ,所以,数列
,所以,数列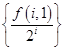 是以2为首项,1为公差的等差数列, 所以,
是以2为首项,1为公差的等差数列, 所以,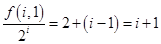 ,所以
,所以 (
(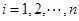 ). (18分)
). (18分)
考点:(1)等差数列的通项公式;(2)等差数列的判定;(3)由递推公式求通项公式.

练习册系列答案
相关题目
 的前
的前 项和记为
项和记为 ,已知
,已知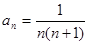 .
.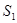 ,
, ,
,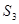 的值,猜想
的值,猜想 所表示的平面区域为
所表示的平面区域为 ,记
,记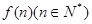
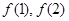 的值及
的值及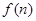 的表达式;
的表达式;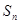 为数列
为数列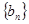 的前
的前 项的和,其中
项的和,其中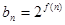 ,问是否存在正整数
,问是否存在正整数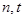 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数 =
= ,求
,求 的值;
的值; )项,且
)项,且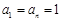 ,对每个i (1≤i≤
,对每个i (1≤i≤ ,i
,i N),均有
N),均有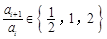 .
.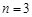 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);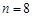 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数.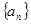 中,
中,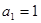 ,
,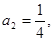 且
且
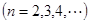 .
.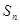 为数列
为数列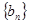 的前
的前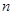 项和,且
项和,且
 .
. ,求数列
,求数列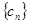 的前
的前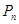 ;
;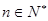 ,有
,有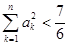 .
.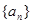 ,
,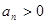 ,
,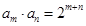 ,
,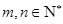 .
.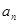 ;
;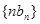 的前
的前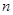 项和为
项和为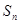 且
且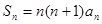 ,求
,求
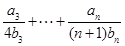 .
.