题目内容
设数列 的首项
的首项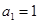 ,前
,前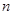 项和为
项和为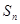 ,且
,且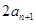 ,
,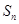 ,
,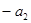 成等差数列,其中
成等差数列,其中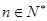 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列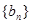 满足:
满足: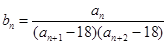 ,记数列
,记数列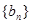 的前
的前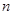 项和为
项和为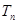 ,求
,求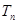 及数列
及数列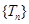 的最大项.
的最大项.
(1)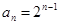 ;(2)
;(2)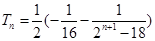 ,最大项是
,最大项是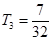 .
.
解析试题分析:(1)根据题意可知 ,考虑到当
,考虑到当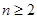 时,
时,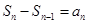 ,因此可以结合条件消去
,因此可以结合条件消去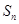 得到数列
得到数列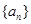 的地推公式:当
的地推公式:当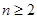 时,
时,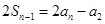 ,
,
∴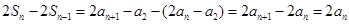 ,∴
,∴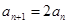 ,容易验证当
,容易验证当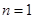 时,上述关系式也成立,从而数列
时,上述关系式也成立,从而数列 是首项为1,公比为2的等比数列,即有
是首项为1,公比为2的等比数列,即有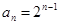 ;(2)根据(1)中求得的通项公式,结合条件
;(2)根据(1)中求得的通项公式,结合条件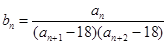 ,因此可以考虑采用裂项相消法来求其前
,因此可以考虑采用裂项相消法来求其前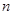 项和:
项和: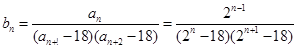
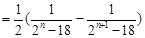

 ,利用作差法来考察数列
,利用作差法来考察数列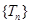 的单调性,可知当
的单调性,可知当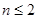 时,
时,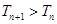 ,即
,即 ;当
;当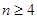 时,也有
时,也有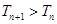 ,但
,但 ;当
;当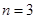 时,
时,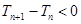 ,
,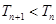 ,即
,即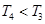 ,因此最大项即为
,因此最大项即为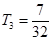 .
.
试题解析:(1)由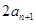 、
、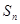 、
、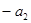 成等差数列知
成等差数列知 , 1分
, 1分
当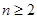 时,
时,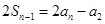 ,∴
,∴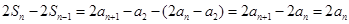 ,
,
∴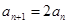 , 4分
, 4分
当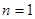 时,由
时,由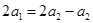 得
得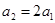 , 5分
, 5分
综上知,对任何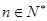 ,都有
,都有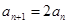 ,又
,又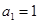 ,∴
,∴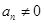 ,
,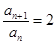 . 6分
. 6分
∴数列 是首项为1,公比为2的等比数列,∴
是首项为1,公比为2的等比数列,∴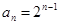 ; 7分
; 7分
(2)
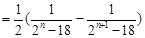 , 10分
, 10分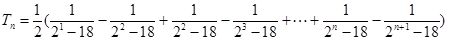
 , 12分
, 12分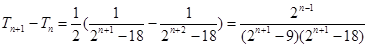 ,
,
当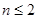 时,
时,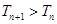 ,即
,即 ;当
;当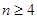 时,也有
时,也有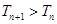 ,但
,但 ;当
;当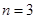 时,
时,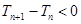 ,
,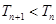 ,即
,即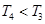 ,∴数列
,∴数列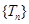

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的一边
的一边 在
在 轴上,另外两个顶点
轴上,另外两个顶点 在函数
在函数 的图象上.若点
的图象上.若点 的坐标为
的坐标为
 且
且  ,记矩形
,记矩形 的周长为
的周长为 ,则
,则

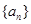 的各项均为正数,公比为
的各项均为正数,公比为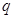 ,前
,前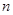 项和为
项和为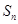 .若对
.若对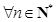 ,有
,有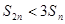 ,则
,则 的前
的前 项和记为
项和记为 ,已知
,已知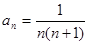 .
.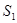 ,
, ,
,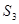 的值,猜想
的值,猜想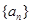 中,
中,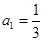 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的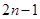 倍(
倍(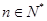 ).
). =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
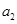 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;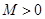 .使
.使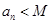 对
对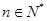 都成立? 若存在,找出
都成立? 若存在,找出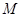 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由. 所表示的平面区域为
所表示的平面区域为 ,记
,记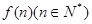
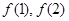 的值及
的值及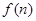 的表达式;
的表达式;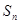 为数列
为数列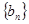 的前
的前 项的和,其中
项的和,其中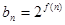 ,问是否存在正整数
,问是否存在正整数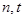 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数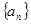 中,
中,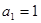 ,
,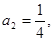 且
且
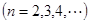 .
.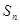 为数列
为数列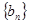 的前
的前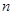 项和,且
项和,且
 .
. ,求数列
,求数列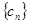 的前
的前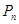 ;
;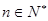 ,有
,有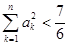 .
.