题目内容
已知数列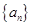 满足对任意的
满足对任意的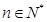 ,都有
,都有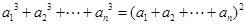 且
且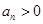 .
.
(1)求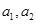 的值;
的值;
(2)求数列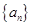 的通项公式
的通项公式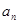 ;
;
(3)设数列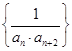 的前
的前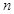 项和为
项和为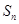 ,不等式
,不等式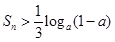 对任意的正整数
对任意的正整数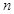 恒成立,求实数
恒成立,求实数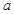 的取值范围.
的取值范围.
(1)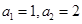 (2)
(2)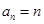 .(3)
.(3)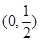
解析试题分析:(1)当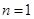 ,
,  时直接代入条件
时直接代入条件 且
且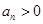 可求
可求
(2)递推一项,然后做差得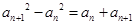 ,所以
,所以
由于a2-a1=1,即当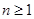 时都有
时都有
所以数列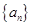 是首项为1,公差为1的等差数列,故
是首项为1,公差为1的等差数列,故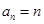
(3)由(2)知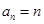 则
则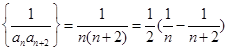
利用裂项相消法得Sn,根据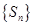 单调递增得
单调递增得
要使不等式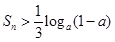 对任意正整数
对任意正整数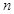 恒成立,只要
恒成立,只要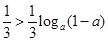
可求得实数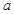 的取值范围是
的取值范围是 .
.
试题解析:((1)当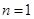 时,有
时,有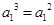 ,由于
,由于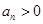 ,所以
,所以
当 时,有
时,有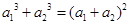 ,将
,将 代入上式,由于
代入上式,由于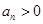 ,所以
,所以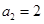
(2)由于 ,①
,①
则有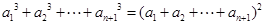 ②
②
②-①,得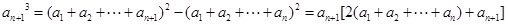
由于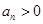 ,所以
,所以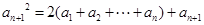 ③
③
同样有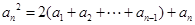 (
( ),④
),④
③-④,得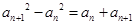 ,所以
,所以
由于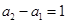 a2-a1=1,即当
a2-a1=1,即当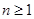 时都有
时都有
所以数列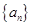 是首项为1,公差为1的等差数列,故
是首项为1,公差为1的等差数列,故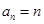
(3)由(2)知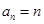
则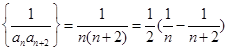
所以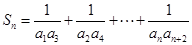

∵ ∴数列
∴数列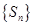 单调递增.
单调递增.
所以
要使不等式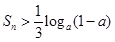 对任意正整数
对任意正整数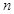 恒成立,只要
恒成立,只要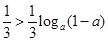
∵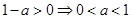
∴ ,即
,即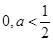 .所以,实数
.所以,实数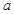 的取值范围是
的取值范围是 .
.
考点:不等式与数列综合题.

练习册系列答案
相关题目
 ,若a6=1,则m所有可能的取值为________________
,若a6=1,则m所有可能的取值为________________ 为正整数时,定义函数
为正整数时,定义函数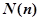 表示
表示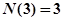 ,
,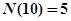 ,….记
,….记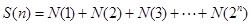 .则
.则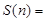 .(用
.(用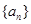 的各项均为正数,公比为
的各项均为正数,公比为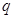 ,前
,前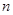 项和为
项和为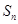 .若对
.若对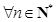 ,有
,有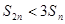 ,则
,则 ,各项均为正数的数列
,各项均为正数的数列 满足
满足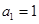 ,
,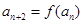 ,若
,若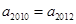 ,则
,则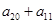 的值是 .
的值是 . 的前
的前 项和记为
项和记为 ,已知
,已知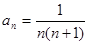 .
.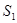 ,
, ,
,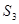 的值,猜想
的值,猜想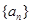 中,
中,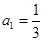 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的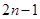 倍(
倍(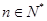 ).
).
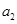 是否为有理数,证明你的结论;
是否为有理数,证明你的结论;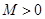 .使
.使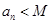 对
对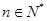 都成立? 若存在,找出
都成立? 若存在,找出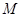 的一个值, 并加以证明; 若不存在,说明理由.
的一个值, 并加以证明; 若不存在,说明理由. )项,且
)项,且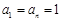 ,对每个i (1≤i≤
,对每个i (1≤i≤ ,i
,i N),均有
N),均有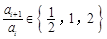 .
.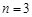 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);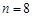 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数.