题目内容
已知数列 的前n项和为
的前n项和为 ,且
,且
(1)求数列 的通项公式;
的通项公式;
(2)若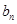 满足
满足 ,求数列
,求数列 的前n项和为
的前n项和为 ;
;
(3)设 是数列
是数列 的前n项和,求证:
的前n项和,求证: 。
。
(1)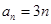 ;(2)
;(2) ;(3)见解析。
;(3)见解析。
解析试题分析:(1)利用 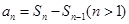 可求得数列
可求得数列 的通项公式,注意验证
的通项公式,注意验证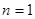 ;(2)由(1)知
;(2)由(1)知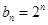 ,即数列
,即数列 为等比数列,利用其前n项和公式进行求和;(3)利用裂项相消求得
为等比数列,利用其前n项和公式进行求和;(3)利用裂项相消求得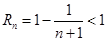 ,再利用函数的单调性可得证。
,再利用函数的单调性可得证。
(1)当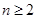 时,
时,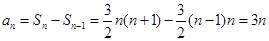 ,
,
当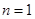 时,
时,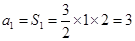 ,也适合上式.
,也适合上式.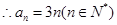 。
。
(2)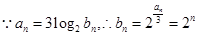 ,
,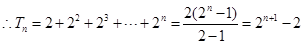
(3) 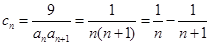 ,
, 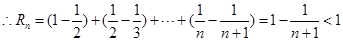
 单调递增,
单调递增,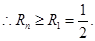 故
故
考点:(1)利用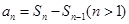 求数列的通项公式;(2)等比数列前其前n项和公式的应用;(3)利用裂项相消进行数列求和。
求数列的通项公式;(2)等比数列前其前n项和公式的应用;(3)利用裂项相消进行数列求和。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 的图象在点
的图象在点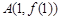 处的切线
处的切线 与直线
与直线 平行,若数列
平行,若数列 的前
的前 项和为
项和为 ,则
,则 的值为 .
的值为 . 中,
中,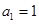 ,
, ,其通项公式
,其通项公式 = .
= . 的前
的前 项和记为
项和记为 ,已知
,已知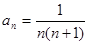 .
.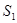 ,
, ,
,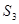 的值,猜想
的值,猜想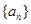 的前n项和
的前n项和 满足
满足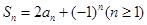
 、
、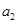 、
、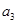 ;
;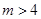 有
有
 =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn< 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m. ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列. 的值;
的值; 的首项和公差都为
的首项和公差都为 的首项和公比都为
的首项和公比都为 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数