题目内容
若变量x，y满足约束条件
，且z=3x+5y，则log3
的最大值为（ ）
|
| z |
| 2 |
| A、18 | ||
| B、2 | ||
| C、9 | ||
D、log3
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，根据z的几何意义，利用数形结合即可得到最大值．
解答：
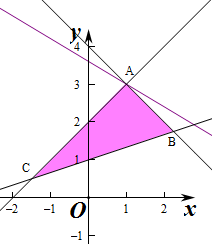解：不等式组对应的平面区域如图：
由z=3x+5y得y=-
x+
，平移直线y=-
x+
，则由图象可知当直线y=-
x+
经过点A时直线y=-
x+
的截距最大，
此时z最大，当经过点B时，直线的截距最小，此时z最小．
由
，解得
，即A（1，3），
此时z=3×1+5×3=18，
则log3
的最大值为log3
=log39=2，
故选：B
解：不等式组对应的平面区域如图：由z=3x+5y得y=-
| 3 |
| 5 |
| z |
| 5 |
| 3 |
| 5 |
| z |
| 5 |
| 3 |
| 5 |
| z |
| 5 |
| 3 |
| 5 |
| z |
| 5 |
此时z最大，当经过点B时，直线的截距最小，此时z最小．
由
|
|
此时z=3×1+5×3=18，
则log3
| z |
| 2 |
| 18 |
| 2 |
故选：B
点评：本题主要考查线性规划的应用以及对数的基本运算，根据z的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
综合自测系列答案
相关题目
在△ABC中，若角A，B，C所对的三边a，b，c成等差数列，给出下列结论：
①b2≥ac；②b2≥
；③
+
＜
；④0＜B≤
．
其中正确的结论是（ ）
①b2≥ac；②b2≥
| a2+c2 |
| 2 |
| 1 |
| a |
| 1 |
| c |
| 2 |
| b |
| π |
| 3 |
其中正确的结论是（ ）
| A、①② | B、②③ | C、③④ | D、①④ |
曲线y=x于y=x3围成的封闭区域的面积是（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
方程x2+y2-2x+6y+m=0表示圆，则实数m的取值范围（ ）
| A、m＞10 | B、m≥10 |
| C、m≤10 | D、m＜10 |