题目内容
由小到大排列的一组数据:x1,x2,x3,x4,x5,其中每个数据都小于-2,则样本2,-x1,x2,x3,-x4,x5的中位数可以表示为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:众数、中位数、平均数
专题:概率与统计
分析:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.根据这个定义求出.
解答:
解:因为x1<x2<x3<x4<x5<-2,题目中数据共有六个,排序后为x1<x3<x5<2<-x4<-x2,
故中位数是按从小到大排列后第三,第四两个数的平均数作为中位数,
故这组数据的中位数是
.
故选:C.
故中位数是按从小到大排列后第三,第四两个数的平均数作为中位数,
故这组数据的中位数是
| 2+x5 |
| 2 |
故选:C.
点评:本题属于基础题,考查了确定一组数据的中位数的能力.要明确定义.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.

练习册系列答案
相关题目
将一个正四面体沿各棱的中点截去四个小三棱锥后得到一个新几何体,将此几何体的任意两个顶点连成一条线段,则其位于原四面体表面的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
以下四个命题中,正确的有几个( )
①直线a,b与平面a所成角相等,则a∥b;
②两直线a∥b,直线a∥平面a,则必有b∥平面a;
③一直线与平面的一斜线在平面a内的射影垂直,则该直线必与斜线垂直;
④两点A,B与平面a的距离相等,则直线AB∥平面a.
①直线a,b与平面a所成角相等,则a∥b;
②两直线a∥b,直线a∥平面a,则必有b∥平面a;
③一直线与平面的一斜线在平面a内的射影垂直,则该直线必与斜线垂直;
④两点A,B与平面a的距离相等,则直线AB∥平面a.
| A、0个 | B、1个 | C、2个 | D、3个 |
某车间加工零件的数量x与加工时间y的统计数据如表
现已求得如表数据的回归方程
=
x+
中
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
| 零件数x(个) | 10 | 20 | 30 |
| 加工时间y(分钟) | 22 | 30 | 38 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| A、84分钟 | B、94分钟 |
| C、102分钟 | D、112分钟 |
学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座,每科一节课,每节至少有一科,且数学、理综不安排在同一节,则不同的安排方法共有( )
| A、36种 | B、30种 |
| C、24种 | D、6种 |
正奇数按下表排列,则数字2013在( )
| 第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
| 第一行 | 1 | 3 | 5 | 7 | |
| 第二行 | 15 | 13 | 11 | 9 | |
| 第三行 | 17 | 19 | 21 | 23 | |
| 第四行 | 31 | 29 | 27 | 25 |
| A、第252行,第2列 |
| B、第252行,第3列 |
| C、第153行,第3列 |
| D、第253行,第4列 |
如图程序的功能是( )


| A、统计十个数据中负数的个数 |
| B、找出十个数据中的负数 |
| C、判断x的符号 |
| D、求十个数据中所有负数的和 |
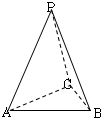 在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是
在三棱锥P-ABC中,已知PA=PB=PC=2,∠BPA=∠BPC=∠CPA=30°,一绳子从A点绕三棱锥侧面一圈回到点A的距离中,绳子最短距离是