题目内容
以下四个命题中，正确的有几个（ ）
①直线a，b与平面a所成角相等，则a∥b；
②两直线a∥b，直线a∥平面a，则必有b∥平面a；
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直；
④两点A，B与平面a的距离相等，则直线AB∥平面a．
①直线a，b与平面a所成角相等，则a∥b；
②两直线a∥b，直线a∥平面a，则必有b∥平面a；
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直；
④两点A，B与平面a的距离相等，则直线AB∥平面a．
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：①直线a，b与平面a所成角相等，则a∥b或为异面直线、相交直线，即可判断出；
②两直线a∥b，直线a∥平面a，则b∥平面a或b?平面α，即可判断出；
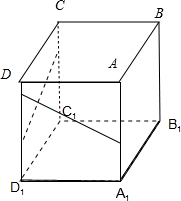
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直，如图所示的正方体，侧面CDD1C1的任意一条直线在底面的射影C1D1与侧面ADD1A1的任意一条直线都垂直，而此两条直线不一定垂直，即可判断出；
④两点A，B与平面a的距离相等，则直线AB∥平面a或AB与平面α相交其交点为线段AB的中点，即可判断出．
②两直线a∥b，直线a∥平面a，则b∥平面a或b?平面α，即可判断出；
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直，如图所示的正方体，侧面CDD1C1的任意一条直线在底面的射影C1D1与侧面ADD1A1的任意一条直线都垂直，而此两条直线不一定垂直，即可判断出；
④两点A，B与平面a的距离相等，则直线AB∥平面a或AB与平面α相交其交点为线段AB的中点，即可判断出．
解答：
解：①直线a，b与平面a所成角相等，则a∥b或为异面直线、相交直线，因此不正确；
②两直线a∥b，直线a∥平面a，则b∥平面a或b?平面α，因此不正确；
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直，如图所示的正方体，侧面CDD1C1的任意一条直线在底面的射影C1D1与侧面ADD1A1的任意一条直线都垂直，而此两条直线不一定垂直，因此不正确；
④两点A，B与平面a的距离相等，则直线AB∥平面a或AB与平面α相交其交点为线段AB的中点，因此不正确．
综上可得：正确的结论为0．
故选：A．
解：①直线a，b与平面a所成角相等，则a∥b或为异面直线、相交直线，因此不正确；②两直线a∥b，直线a∥平面a，则b∥平面a或b?平面α，因此不正确；
③一直线与平面的一斜线在平面a内的射影垂直，则该直线必与斜线垂直，如图所示的正方体，侧面CDD1C1的任意一条直线在底面的射影C1D1与侧面ADD1A1的任意一条直线都垂直，而此两条直线不一定垂直，因此不正确；
④两点A，B与平面a的距离相等，则直线AB∥平面a或AB与平面α相交其交点为线段AB的中点，因此不正确．
综上可得：正确的结论为0．
故选：A．
点评：本题综合考查了空间两条直线的位置关系及其判定方法，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
设a，b是两条不同的直线，α，β是两个不同的平面，则（ ）
| A、若a∥α，b∥α，则a∥b |
| B、若a∥α，a∥β，则α∥β |
| C、若a∥b，a⊥α，则b⊥α |
| D、若a∥α，α⊥β，则α⊥β |
已知平面向量|
|，|
|满足|
|=4，|
|=3，向量
与
的夹角是60°，则|
+
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列各式中，值为
的是（ ）
| 1 |
| 2 |
| A、sin15°•cos15° | ||||
B、2cos2
| ||||
C、
| ||||
D、
|
由小到大排列的一组数据：x1，x2，x3，x4，x5，其中每个数据都小于-2，则样本2，-x1，x2，x3，-x4，x5的中位数可以表示为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=（2，1），
=（3，4），则向量
在向量
方向上正射影的数量为（ ）
| a |
| b |
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
| D、5 |
现有60件产品，编号从1到60，若用系统抽样方法从中抽取6件检验，则所抽到的个体编号可能是（ ）
| A、5，10，15，20，25，30 |
| B、2，14，26，28，42，56 |
| C、5，8，31，36，48，54 |
| D、3，13，23，33，43，53 |