题目内容
14.在△ABC中,a、b、c分别为角ABC所对的边,且$\sqrt{3}$acosC=csinA.(1)求角C的大小.
(2)若c=2$\sqrt{7}$,且△ABC的面积为6$\sqrt{3}$,求a+b的值.
分析 (1)已知等式变形后利用正弦定理化简,整理后再利用同角三角函数间的基本关系求出tanC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;
(2)由余弦定理可得:28=(a+b)2-3ab,由三角形面积公式可解得:ab=24,进而解得a+b的值.
解答 解:(1)由csinA=$\sqrt{3}$acosC,结合正弦定理得,$\frac{a}{sinA}=\frac{c}{\sqrt{3}cosC}=\frac{c}{sinC}$,
∴sinC=$\sqrt{3}$cosC,即tanC=$\sqrt{3}$,
∵0<C<π,
∴C=$\frac{π}{3}$;
(2)∵C=$\frac{π}{3}$,c=2$\sqrt{7}$,
∴由余弦定理可得:28=a2+b2-ab=(a+b)2-3ab,
∵△ABC的面积为6$\sqrt{3}$=$\frac{1}{2}$absinC=$\frac{1}{2}×\frac{\sqrt{3}}{2}$ab,
解得:ab=24,
∴28=(a+b)2-3ab=(a+b)2-72,解得a+b=10.
点评 此题考查了正弦定理,余弦定理、三角形面积公式以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
18. 如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
 如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )
如图,已知点D为三角形ABC边BC上一点,$\overrightarrow{BD}$=3$\overrightarrow{DC}$,En(n∈N*)为AC边上的一列点,满足$\overrightarrow{{E}_{n}A}$=$\frac{1}{4}$an+1$\overrightarrow{{E}_{n}B}$-(3an+2)$\overrightarrow{{E}_{n}D}$,其中实数列{an}中,an>0,a1=1,则{an}的通项公式为( )| A. | 3•2n-1-1 | B. | 2n-1 | C. | 3n-2 | D. | 2•3n-1-1 |
2.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}++\frac{1}{119}$的值的一个程序框图,其中判断框内可以填入的条件是( )
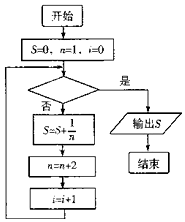

| A. | i≤119? | B. | i≥119? | C. | i≤60? | D. | i≥60? |