题目内容
12.已知函数f(x)=|x-1|-2|x+1|的最大值为k.(1)求k的值;
(2)若a,b,c∈R,$\frac{{{a^2}+{c^2}}}{2}+{b^2}=k$,求b(a+c)的最大值.
分析 (1)根据分段函数的单调性求出函数的最大值,即可求出k的值,
(2)根据基本不等式即可求出答案
解答 解:(1)由于f(x)=$\left\{\begin{array}{l}{-x-3,x≥1}\\{-3x-1,-1<x<1}\\{x+3,x≤-1}\end{array}\right.$,
当x≥-1时,f(x)max=f(1)=1-3=-4,
当-1<x<1时,f(x)<f(-1)=3-1=2,
当x≤-1时,f(x)max=f(-1)=-1+3=2,
所以k=f(x)max=f(-1)=2,
(2)由已知$\frac{{{a^2}+{c^2}}}{2}+{b^2}=2$,有(a2+b2)+(b2+c2)=4,
因为a2+b2≥2ab(当a=b取等号),b2+c2≥2bc(当b=c取等号),
所以(a2+b2)+(b2+c2)=4≥2(ab+bc),即ab+bc≤2,
故[b(a+c)]max=2.
点评 本题考查了绝对值不等式的解法和基本不等式的应用,属于中档题

练习册系列答案
相关题目
2.如图给出的是计算$1+\frac{1}{3}+\frac{1}{5}++\frac{1}{119}$的值的一个程序框图,其中判断框内可以填入的条件是( )
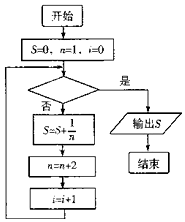

| A. | i≤119? | B. | i≥119? | C. | i≤60? | D. | i≥60? |
20.若$\frac{1+mi}{1-i}$为纯虚数,则m的值为( )
| A. | m=-1 | B. | m=1 | C. | m=2 | D. | m=-2 |
17.已知f(x)=$\frac{a}{2}$-$\frac{3}{{2}^{x}+1}$是R上的奇函数,则f(a)的值为( )
| A. | $\frac{7}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |