题目内容
若P为f（x）=ex上任意一点，则点P到直线x-y-5=0的距离的最小值为 ．
考点：点到直线的距离公式
专题：直线与圆
分析：过点P的切线与直线x-y-5=0平行时，两平行线之间的距离即为曲线上的点到直线的最短距离，求出点P的坐标，由点到直线的距离公式求解即可．
解答：
解：过点P的切线与直线x-y-5=0平行时，
两平行线之间的距离即为曲线上的点到直线的最短距离，
求导数可得f′（x）=ex，
令f′（x）=ex=1，解得x=0，可得P（0，1）
∴点P到直线x-y-5=0的最小距离为
=3
故答案为：3
．
两平行线之间的距离即为曲线上的点到直线的最短距离，
求导数可得f′（x）=ex，
令f′（x）=ex=1，解得x=0，可得P（0，1）
∴点P到直线x-y-5=0的最小距离为
| |0-1-5| | ||
|
| 2 |
故答案为：3
| 2 |
点评：本题考查点到直线的距离公式，涉及导数的几何意义，属基础题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
相关题目
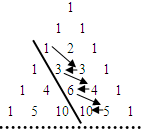如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10…，记其前n项和为Sn，则S41的值为已知A（1，-2），若向量
与
=（2，-3）反向，|
|=4
，则点B的坐标为（ ）
| AB |
| a |
| AB |
| 13 |
| A、（10，7） |
| B、（-10，7） |
| C、（7，-10） |
| D、（-7，10） |