题目内容
10.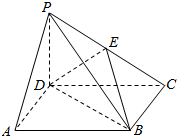 如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.(1)证明:PA∥平面EDB;
(2)求直线PB与平面ABCD所成角的正弦值.
分析 (1)连接AC交BD于O.连接EO,由三角形中位线定理得PA∥EO,由此能证明PA∥平面EDB.
(2)由PD⊥底面ABCD,得∠PBD为直线PB与平面ABCD所成角,由此能求出直线PB与平面ABCD所成角的正弦值.
解答  证明:(1)如图,连接AC交BD于O.连接EO.
证明:(1)如图,连接AC交BD于O.连接EO.
∵底面ABCD是正方形,
∴点O是AC的中点,
在△PAC中,∵E是PC的中点,∴EO是中位线,
∴PA∥EO.
而EO?平面EDB,且PA?平面EDB.
所以PA∥平面EDB.(6分)
解:(2)∵四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,
∴由题意PD⊥底面ABCD,∴∠PBD为直线PB与平面ABCD所成角,(8分)
设PD=DC=1,在Rt△PBD中,BD=$\sqrt{1+1}$=$\sqrt{2}$,PB=$\sqrt{2+1}=\sqrt{3}$,
∴sin∠PBD=$\frac{PD}{PB}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴直线PB与平面ABCD所成角的正弦值为$\frac{\sqrt{3}}{3}$.(12分)
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
20.某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为( )
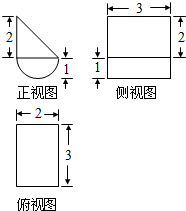

| A. | 16+6$\sqrt{2}$+4π | B. | 16+6$\sqrt{2}$+3π | C. | 10+6$\sqrt{2}$+4π | D. | 10+6$\sqrt{2}$+3π |
1.若关于x的方程2x3-3x2+a=0在区间[-2,2]上仅有一个实根,则实数a的取值范围为( )
| A. | (-4,0]∪[1,28) | B. | [-4,28] | C. | [-4,0)∪(1,28] | D. | (-4,28) |
18.一个几何体的三视图如图所示,则该几何体的体积为( )
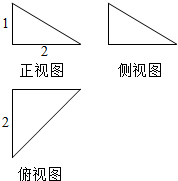

| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 2 |