题目内容
7.从甲、乙两部分中各任选10名员工进行职业技能测试,测试成绩(单位:分)数据的茎叶图如图1所示.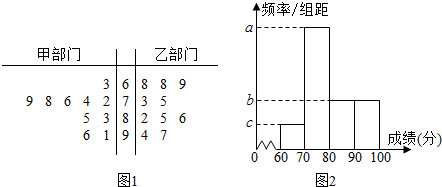
(Ⅰ)分别求出甲、乙两组数据的中位数,并比较两组数据的分散程度(只需给出结论);
(Ⅱ)甲组数据频率分别直方图如图2所示,求a,b,c的值;
(Ⅲ)从甲、乙两组数据中各任取一个,求所取两数之差的绝对值大于20的概率.
分析 (Ⅰ)由茎叶图能求出甲、乙两组数据的中位数,由茎叶图得到甲组数据比乙组数据更集中.
(Ⅱ)由茎叶图分别示求出甲组数据在[60,70)、[70,80)、[80,90)和[90,100)间的频数,再由频率分布直方图能求出a,b,c.
(Ⅲ)从甲、乙两组数据中各任取一个,求出基本事件总数,列举出所取两数之差的绝对值大于20包含的基本事件个数,由此能求出所取两数之差的绝对值大于20的概率.
解答 解:(Ⅰ)由茎叶图得甲两组数据的中位数为:$\frac{78+79}{2}$=78.5,
乙两组数据的中位数为:$\frac{75+82}{2}$=78.5,
由茎叶图得到甲组数据比乙组数据更集中.
(Ⅱ)由茎叶图得甲组数据在[60,70)间的频率为1,
在[70,80)间的频数为5,在[80,90)和[90,100)间的频数都是2,
∴由频率分布直方图得a=$\frac{1}{10}$×$\frac{1}{10}$=0.01,b=$\frac{5}{10}×\frac{1}{10}$=0.01,c=$\frac{2}{10}×\frac{1}{10}$=0.02.
(Ⅲ)从甲、乙两组数据中各任取一个,基本事件总数n=10×10=100,
所取两数之差的绝对值大于20包含的基本事件有:(63,85),(63,86),(63,94),(63,97),(72,94),(72,97),
(74,97),(76,97),(68,91),(68,91),(68,96),(68,96),(69,91),(69,96),(73,96),(75,96),
共16个,
∴所取两数之差的绝对值大于20的概率p=$\frac{16}{100}=0.16$.
点评 本题考查茎叶图和频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

 阅读快车系列答案
阅读快车系列答案
| A. | $\frac{4}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | 2 |
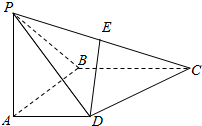 如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.
如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点.