题目内容
已知向量
=（1+cosωx，1），
=（1，a+
sinωx）（ω为常数且ω＞0），函数f（x）=
•
在R上的最大值为2．
（Ⅰ）求实数a的值；
（Ⅱ）把函数y=f（x）的图象向右平移
个单位，可得函数y=g（x）的图象，若y=g（x）在[0，
]上为增函数，求ω取最大值时的单调增区间．
| a |
| b |
| 3 |
| a |
| b |
（Ⅰ）求实数a的值；
（Ⅱ）把函数y=f（x）的图象向右平移
| π |
| 6ω |
| π |
| 4 |
考点：函数y=Asin（ωx+φ）的图象变换,平面向量数量积的运算
专题：三角函数的图像与性质
分析：（Ⅰ）通过向量的数量积以及两角和与差的三角函数，化为一个角的一个三角函数的形式，通过函数的最大值，即可求实数a的值；
（Ⅱ）通过函数y=f（x）的图象向右平移
个单位，可得函数y=g（x）的图象，利用y=g（x）在[0，
]上为增函数，以及函数的周期，即可求ω取最大值，求出函数的单调增区间．
（Ⅱ）通过函数y=f（x）的图象向右平移
| π |
| 6ω |
| π |
| 4 |
解答：
解：（Ⅰ）函数f（x）=
•
=1+cosωx+a+
sinx=2sin（ωx+
）+a+1，…（3分）
∵函数f（x）在R上的最大值为2，
∴3+a=2故a=-1…（4分）
（Ⅱ）由（Ⅰ）知：f（x）=2sin（ωx+
），
把函数f（x）=2sin（ωx+
）的图象向右平移
个单位，可得函数y=g（x）=2sinωx…（7分）
又∵y=g（x）在[0，
]上为增函数，
∴g（x）的周期T=
≥π即ω≤2．
∴ω的最大值为2…（10分）
此时单调增区间为[kπ-
，kπ+
]，k∈Z…（12分）
| a |
| b |
| 3 |
| π |
| 6 |
∵函数f（x）在R上的最大值为2，
∴3+a=2故a=-1…（4分）
（Ⅱ）由（Ⅰ）知：f（x）=2sin（ωx+
| π |
| 6 |
把函数f（x）=2sin（ωx+
| π |
| 6 |
| π |
| 6ω |
又∵y=g（x）在[0，
| π |
| 4 |
∴g（x）的周期T=
| 2π |
| ω |
∴ω的最大值为2…（10分）
此时单调增区间为[kπ-
| π |
| 4 |
| π |
| 4 |
点评：本题考查向量的数量积以及两角和与差的三角函数就三角函数的图象的平移，函数的基本性质，考查计算能力．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
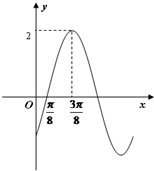函数f（x）=Msin（ωx-