题目内容
设奇函数f(x)定义在(-∞,0)∪(0,+∞)上,f(x)在(0,+∞)上为增函数,且f(1)=0,则不等式
<0的解集为( )
| 3f(x)-2f(-x) |
| 5x |
| A、(-1,0)∪(1,+∞) |
| B、(-∞,-1)∪(0,1) |
| C、(-∞,-1)∪(1,+∞) |
| D、(-1,0)∪(0,1) |
考点:奇偶性与单调性的综合
专题:数形结合,函数思想,函数的性质及应用
分析:根据已给的函数性质,结合奇函数的图象关于原点对称,可画出其图象,注意过点(1,0)和(-1,0),且在(-∞,0)和(0,+∞)上有相同的单调性,再将要解的不等式据函数性质化简为xf(x)<0,据图可得不等式的解集.
解答:
解:∵奇函数f(x)定义在(-∞,0)∪(0,+∞)上,在(0,+∞)上为增函数,且f(1)=0,
∴函数f(x)的关于原点对称,且在(-∞,0)上也是增函数,过点(-1,0),所以可将函数f(x)的图象画出,大致如下
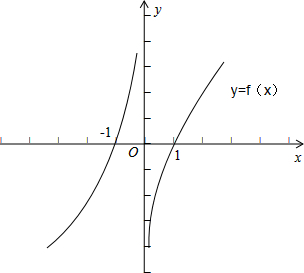
∵f(-x)=-f(x),∴不等式
<0可化为
<0,即xf(x)<0,不等式的解集即为自变量与函数值异号的x的范围,
据图象可知x∈(-1,0)∪(0,1).
故选D
∴函数f(x)的关于原点对称,且在(-∞,0)上也是增函数,过点(-1,0),所以可将函数f(x)的图象画出,大致如下
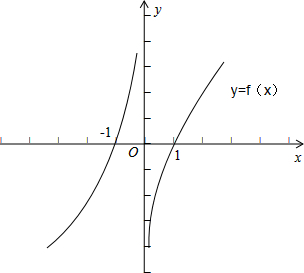
∵f(-x)=-f(x),∴不等式
| 3f(x)-2f(-x) |
| 5x |
| f(x) |
| x |
据图象可知x∈(-1,0)∪(0,1).
故选D
点评:此题考查了抽象函数的奇偶性与单调性,解题抓住两点:①抽象函数直观化,即借助于图象表现其性质,借助于图象求解;②函数的奇偶性与单调性的关系,奇函数在关于原点对称的区间上具有相同的单调性,偶函数的单调性则相反.

练习册系列答案
相关题目
阅读如图所示程序,则输出的s的值是( )


| A、17 | B、19 | C、21 | D、23 |
复数z=i(-3-2i)(i为虚数单位)在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
计算:C22+C32+…+C102( )
| A、160 | B、165 |
| C、55 | D、110 |
已知在△ABC中,点D在BC边上,且
=2
=r
+s
,则2r+s的值是( )
| CD |
| DB |
| AB |
| AC |
| A、0 | ||
B、
| ||
| C、2 | ||
D、
|
函数f(x)=ax+logax在[1,2]上的最大值和最小值之差为|a2-a|+1,则a值为( )
A、2或
| ||
| B、2或4 | ||
C、
| ||
| D、2 |
 如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )
如图所示,AB为⊙O直径,CD切⊙O于D,AB延长线交CD于点C,若∠CAD=25°,则∠C为( )| A、45° | B、40° |
| C、35° | D、30° |
 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=