题目内容
设集合A={x|x2-x-6≤0}，B={x|x2-5x≥0}，则A∩（∁RB）= ．
考点：一元二次不等式的解法,交、并、补集的混合运算
专题：计算题
分析：化简A、B，求出（∁RB），再计算A∩（∁RB）
解答：
解：∵A={x|x2-x-6≤0}={x|（x-3）（x+2）≤0}={x|-2≤x≤3}，
B={x|x2-5x≥0}={x|x（x-5）≥0}={x|x≤0或x≥5}，
∴（∁RB）={x|0＜x＜5}，
∴A∩（∁RB）={x|0＜x≤3}；
故答案为：（0，3]．
B={x|x2-5x≥0}={x|x（x-5）≥0}={x|x≤0或x≥5}，
∴（∁RB）={x|0＜x＜5}，
∴A∩（∁RB）={x|0＜x≤3}；
故答案为：（0，3]．
点评：本题利用集合的运算考查了一元二次不等式的解法问题，是基础题．
练习册系列答案
相关题目
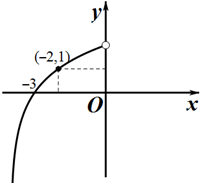已知函数f（x）是定义域为R的奇函数．当x＜0时，f（x）=loga（x+b），图象如图所示．