题目内容
已知矩阵A=
,A的一个特征值λ=2,其对应的特征向量是
=
(Ⅰ)求矩阵A;
(Ⅱ)若向量
=
,计算A4
的值.
|
| a1 |
|
(Ⅰ)求矩阵A;
(Ⅱ)若向量
| β |
|
| β |
考点:几种特殊的矩阵变换,特征向量的定义,特征值、特征向量的应用
专题:矩阵和变换
分析:(1)解法一:利用特征值与特征向量的定义,建立方程组,求出a、b的值,即可求得矩阵A;解法二:首先写出矩阵的特征多项式,然后利用特征值与特征向量的定义,建立方程组,求出a、b的值,即可求得矩阵A;
(2)利用特征向量的性质计算,先利用特征向量表示向量
,然后把A4
的值的问题转化成求有关特征向量的计算问题.
(2)利用特征向量的性质计算,先利用特征向量表示向量
| α2 |
| β |
解答:
解:(I)解法一:由已知可得
=2
∴
解之得
∴A=
解法二:矩阵的特征多项式为f(λ)=
,
∵A的一个特征值为λ=2,其对应的特征向量为
=
∴λ,
满足方程组
∴
∴
∴A=
(II)由f(λ)=(λ-1)(λ-4)+2=0,可得λ1=2,λ2=3
当λ2=3代入
得
∴
=
令β=m
+n
∴
=m
+n
∴
,∴
∴
=3
+
∴A4β=m
+n
=3×24
+1×34
=
+
=
|
|
|
∴
|
解之得
|
∴A=
|
解法二:矩阵的特征多项式为f(λ)=
|
∵A的一个特征值为λ=2,其对应的特征向量为
| α1 |
|
∴λ,
| α1 |
|
∴
|
∴
|
∴A=
|
(II)由f(λ)=(λ-1)(λ-4)+2=0,可得λ1=2,λ2=3
当λ2=3代入
|
|
∴
| α2 |
|
令β=m
| α1 |
| α2 |
∴
|
|
|
∴
|
|
∴
|
|
|
∴A4β=m
| λ | 4 1 |
| α1 |
| λ | 4 2 |
| α2 |
|
|
|
|
|
点评:本题主要考查了矩阵的性质和应用,考查了特征值、特征向量的运用,解答此题的关键是要注意公式的灵活运用.

练习册系列答案
相关题目
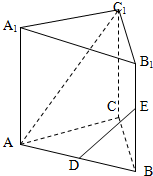 如图,直三棱柱ABC-A1B1C1中,AA1=AC=AB=1,BC=
如图,直三棱柱ABC-A1B1C1中,AA1=AC=AB=1,BC= 将自然1,2,3,4…排成数阵(如图),在2处转第一个弯,在3转第二个弯,在5转第三个弯,….,则第20个转弯处的数为
将自然1,2,3,4…排成数阵(如图),在2处转第一个弯,在3转第二个弯,在5转第三个弯,….,则第20个转弯处的数为