题目内容
已知一个回归方程为
=1.5x+45，x∈{1，7，5，13，19}，则
=（ ）
 |
| y |
. |
| y |
| A、9 | B、45 |
| C、58.5 | D、1.5 |
考点：线性回归方程
专题：概率与统计
分析：求出
=
（1+7+5+13+19）=9，代入回归方程为
=1.5x+45，能求出
．
. |
| x |
| 1 |
| 5 |
|
| y |
. |
| y |
解答：
解：∵
=
（1+7+5+13+19）=9，
回归方程为
=1.5x+45，
∴
=1.5×9+45=58.5．
故选：C．
. |
| x |
| 1 |
| 5 |
回归方程为
|
| y |
∴
. |
| y |
故选：C．
点评：本题考查
的求法，是基础题，解题时要认真审题，注意线性回归方程的合理运用．
. |
| y |
练习册系列答案
相关题目
化简
•
的结果为（ ）
| -a |
| 3 | a |
A、-a
| ||
B、-(-a)
| ||
C、(-a)
| ||
D、-a
|
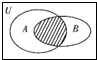设全集U=R，A={x∈Z|-2≤x≤2}，B={x∈R|x2+3x＜0}，则如图中阴影部分表示的集合为（ ）| A、{-1} |
| B、{-2，-1} |
| C、{-2，-1，0} |
| D、（-2，-1） |
（
）2013等于（ ）
| 1+i |
| 1-i |
| A、i | B、-i | C、1 | D、-1 |
在等差数列{an}中，a1=1，a4=7，则公差d为（ ）
| A、4 | B、6 | C、1 | D、2 |
若x∈[0，
]，则使等式cos（πcosx）=0成立的x的值是（ ）
| 3π |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f（x）=x3+ax2+b的图象在点P （1，0）处的切线与直线3x+y=0平行．则a、b的值分别为（ ）
| A、-3，2 | B、-3，0 |
| C、3，2 | D、3，-4 |
在△ABC中，已知a=1，b=2，C=
，则c=（ ）
| π |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
| D、5 |