题目内容
8.设函数y=4x-3•2x+3的值域为[1,7],若定义域为(-∞,0]∪[a,2],求实数a的取值范围.分析 运用换元法,令t=2x,t>0,则y=t2-3t+3,作出y=t2-3t+3在t>0的图象,求出y=1和y=7的交点,由题意可得[2,4]?[2a,4]?[3,4],可得a的不等式,解不等式可得所求范围.
解答 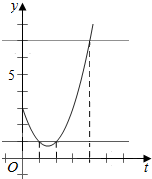 解:令t=2x,t>0,则y=t2-3t+3,
解:令t=2x,t>0,则y=t2-3t+3,
作出y=t2-3t+3在t>0的图象,
由x∈(-∞,0],可得t∈(0,1],
又x∈[a,2],可得t∈[2a,4],
由值域可得y的最小值我,最大值为7,
当t=3时,y=3,即有[2,4]?[2a,4]?[3,4],
即有2≤2a≤3,解得1≤a≤log23,
即有a的范围是[1,log23].
点评 本题考查可化为二次函数的值域问题,注意运用换元法,考查数形结合的思想方法,考查运算能力,属于中档题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
18.汽车发动机排量可以分为两大类,高于1.6L的称为大排量,否则称为小排量,加油时,有92号与95号两种汽油可供选择,某汽车相关网站的注册会员中,有300名会员参与了网络调查,结果如下:
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(Ⅰ)根据此次调查,是否有95%的把握认为该网站会员给汽车加油时进行的型号选择与汽车排量有关?
(Ⅱ)从调查的大排量汽车中按“加油类型”用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个整体,从中任取抽取3辆汽车,求这3辆汽车都是“加92号汽油”的概率.
| 汽车排量 加油类型 | 小排量 | 大排量 |
| 92号 | 160 | 96 |
| 95号 | 20 | 24 |
| P(K2)≥k | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(Ⅱ)从调查的大排量汽车中按“加油类型”用分层抽样的方法抽取一个容量为5的样本,将该样本看成一个整体,从中任取抽取3辆汽车,求这3辆汽车都是“加92号汽油”的概率.
17.已知函数f(x)在其定义域(-∞,0)上是减函数,且f(1-m)<f(m-3),则实数m的取值范围是( )
| A. | (-∞,2) | B. | (0,1) | C. | (0,2) | D. | (1,2) |
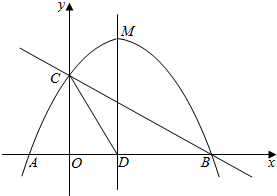 如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).
如图,抛物线y=-$\frac{1}{2}$x2+mx+n与x轴交于点A、B两点,与y轴交于点C,其对称轴与x轴的交点为D,已知A(-1,0),C(0,2).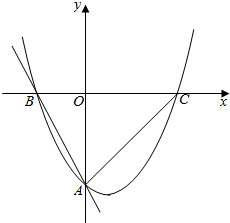 如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点
如图,抛物线y=$\frac{1}{2}{x}^{2}$+bx+c与直线y=-2x-4交y轴于点A,交x轴于点B,抛物线与x轴的另一个交点为C,O为坐标原点