题目内容
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的方程是$y=\sqrt{3}x$,它的一个焦点落在抛物线y2=16x的准线上,则双曲线的方程为( )| A. | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B. | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
分析 利用抛物线的准线方程,推出双曲线的焦点坐标,利用双曲线的渐近线方程,求解即可.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的方程是$y=\sqrt{3}x$,可得b=$\sqrt{3}$a,
它的一个焦点落在抛物线y2=16x的准线上,可得c=4,即16=a2+b2,
a=2,b=2$\sqrt{3}$.
所求的双曲线方程为:$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$.
故选:C.
点评 本题考查抛物线以及双曲线的简单性质的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.设F(c,0)是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,$P(\frac{a^2}{c},\frac{{\sqrt{2}a}}{2})$为直线上一点,且直线垂直于x轴,垂足为M,若△PMF等腰三角形,则E的离心率为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}$ |
1.某化肥厂生产甲、乙两种混合肥料,需要A、B两种主要原料,生产1吨甲种肥料和生产1吨乙种肥料所需两种原料的吨数如下表所示:
每日可用A种原料12吨,B种原料8吨,已知生产1吨甲种肥料可获利润3万元;生产1吨乙种肥料可获利润4万元,分别用x,y表示计划生产甲、乙两种肥料的吨数.
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问每日分别生产甲、乙两种肥料各多少吨,能够产生最大利润?并求出此最大利润.
| 原料 肥料 | A | B |
| 甲 | 3 | 1 |
| 乙 | 2 | 2 |
(1)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(2)问每日分别生产甲、乙两种肥料各多少吨,能够产生最大利润?并求出此最大利润.
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,且F2为抛物线y2=24x的焦点,设点P为两曲线的一个公共点,若△PF1F2的面积为36$\sqrt{6}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | B. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
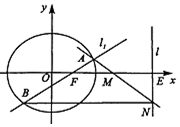 已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.
已知椭圆$E:\frac{x^2}{5}+\frac{y^2}{4}=1$的右焦点为F,设直线l:x=5与x轴的交点为E,过点F且斜率为k的直线l1与椭圆交于A,B两点,M为线段EF的中点.