题目内容
6．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点分别为F1、F2，且F2为抛物线y2=24x的焦点，设点P为两曲线的一个公共点，若△PF1F2的面积为36$\sqrt{6}$，则双曲线的方程为（ ）| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | B． | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 | C． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
分析 利用△PF1F2的面积为36$\sqrt{6}$，求出P的坐标，利用双曲线的定义，求出a，即可求出双曲线的方程．
解答 解：由题意，F2（6，0），
设P（m，n），则
∵△PF1F2的面积为36$\sqrt{6}$，
∴$\frac{1}{2}×12×|n|$=36$\sqrt{6}$，∴|n|=6$\sqrt{6}$，
∴m=9，
取P（9，6$\sqrt{6}$），则2a=$\sqrt{（9+6）^{2}+（6\sqrt{6}）^{2}}$-$\sqrt{（9-6）^{2}+（6\sqrt{6}）^{2}}$=6，
∴a=3，b=3$\sqrt{3}$，
∴双曲线的方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1，
故选A．
点评 本题考查双曲线的方程与性质，考查三角形面积的计算，属于中档题．
练习册系列答案
相关题目
16．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线的方程是$y=\sqrt{3}x$，它的一个焦点落在抛物线y2=16x的准线上，则双曲线的方程为（ ）
| A． | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B． | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C． | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D． | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
17．已知函数f（x）满足如下条件：①任意x∈R，有f（x）+f（-x）=0成立；②当x≥0时，f（x）=$\frac{1}{2}$（|x-m2|+|x-2m2|-3m2）；③任意x∈R，有f（x）≥f（x-1）成立．则实数m的取值范围（ ）
| A． | $[{-\frac{{\sqrt{6}}}{6}，\frac{{\sqrt{6}}}{6}}]$ | B． | $[{-\frac{1}{6}，\frac{1}{6}}]$ | C． | $[{-\frac{{\sqrt{3}}}{3}，\frac{{\sqrt{3}}}{3}}]$ | D． | $[{-\frac{1}{3}，\frac{1}{3}}]$ |
1．复数z=$\frac{1+i}{i}$，则|z|=（ ）
| A． | $\sqrt{2}$ | B． | 2 | C． | -$\sqrt{2}$ | D． | 1-i |
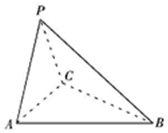如图，三棱锥P-ABC中，PA=PC，底面ABC为正三角形．
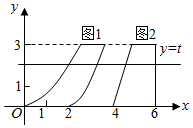我国南北朝时代的数学家祖暅提出体积的计算原理（祖暅原理）：“幂势既同，则积不容 异”．“势’’即是高，“幂”是面积．意思是：如果两等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等，类比祖暅原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个上底为l的梯形，且当实数t取[0，3]上的任意值时，直线y=t被图l和图2所截得的两线段长始终相等，则图l的面积为$\frac{9}{2}$．