题目内容
11.已知函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1,x2(0<x1<x2<1)且满足f(x1)=f(x2),若k=5($\frac{{x}_{1}+{x}_{2}}{2}$+$\sqrt{{x}_{1}{x}_{2}}$),且k为整数时,则k的值为( )(参考数据:e≈2.72)| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 推导出f′(x)=1+lnx,x>0,由f′(x)=0,得x=$\frac{1}{e}$,由x1lnx1=x2lnx2,得0<x1<$\frac{1}{e}$<x2<1,由由$\frac{{x}_{1}+{x}_{2}}{2}>\frac{1}{e}$,${x}_{2}>\frac{2}{e}-{x}_{1}$,得到$\frac{{x}_{1}+{x}_{2}}{2}+\sqrt{{x}_{1}{x}_{2}}$<$\frac{2}{e}$,由此能求出k为整数时,k的值.
解答 解:∵f(x)=xlnx,∴f′(x)=1+lnx,x>0,
由f′(x)=0,得x=$\frac{1}{e}$,
∵函数f(x)=xlnx的图象上有A、B两点,其横坐标为x1,x2(0<x1<x2<1)且满足f(x1)=f(x2),
∴x1lnx1=x2lnx2,
(0<x1<$\frac{1}{e}$<x2<1),如图所示,
由$\frac{{x}_{1}+{x}_{2}}{2}>\frac{1}{e}$,${x}_{2}>\frac{2}{e}-{x}_{1}$,
$\frac{{x}_{1}+{x}_{2}}{2}+\sqrt{{x}_{1}{x}_{2}}$<$\frac{{x}_{1}+(\frac{2}{e}-{x}_{1})}{2}$+$\sqrt{{x}_{1}(\frac{2}{e}-{x}_{1})}$=$\frac{1}{e}+\sqrt{\frac{2}{e}{x}_{1}-{{x}_{1}}^{2}}$,
∵t=$\frac{1}{e}+\sqrt{\frac{2}{e}{x}_{1}-{{x}_{1}}^{2}}$关于x1单调递减,0<x1<$\frac{1}{e}$,
∴$\frac{{x}_{1}+{x}_{2}}{2}+\sqrt{{x}_{1}{x}_{2}}$<$\frac{2}{e}$,∴5($\frac{{x}_{1}+{x}_{2}}{2}$+$\sqrt{{x}_{1}{x}_{2}}$)<$\frac{10}{e}≈3.7$,
∴k≤3.
∴k为整数时,则k的值为3.
故选:C.
点评 本题考查整数的取值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

| A. | $\frac{x^2}{8}-\frac{y^2}{24}=1$ | B. | $\frac{x^2}{24}-\frac{y^2}{8}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
| A. | 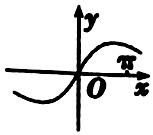 | B. |  | ||
| C. | 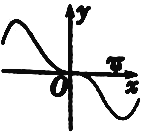 | D. | 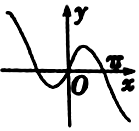 |
| A. | $\sqrt{2}$ | B. | 2 | C. | -$\sqrt{2}$ | D. | 1-i |