题目内容
5.已知动圆M过定点F(1,0),且与直线x=-1相切.(1)求动圆圆心M的轨迹C的方程;
(2)过点F且斜率为2的直线交轨迹C于S,T两点,求弦ST的长度;
(3)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.
分析 (1)根据抛物线的定义和题设中的条件可知点M是以F(1,0)为焦点,以x=-1为准线的抛物线,焦点到准线的距离p=2,进而求得抛物线方程.
(2)直线方程为y=2(x-1),代入y2=4x,可得x2-3x+1=0,利用抛物线的定义,即可求弦ST的长度;
(3)设P(x1,y1),Q(x2,y2),由题意可知y1+y2≠0,y1y2<0.利用角平分线的性质可得kPB=-kQB,可化为化为4+y1y2=0.又直线PQ的方程代入化简整理为y(y1+y2)+4=4x,令y=0,则x=1即可得到定点.
解答 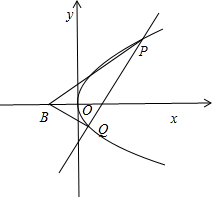 (1)解:由已知,点M到直线x=-1的距离等于到点(1,0)的距离,所以点M是以F(1,0)为焦点,以x=-1为准线的抛物线,焦点到准线的距离p=2,
(1)解:由已知,点M到直线x=-1的距离等于到点(1,0)的距离,所以点M是以F(1,0)为焦点,以x=-1为准线的抛物线,焦点到准线的距离p=2,
∴点M的轨迹方程为y2=4x;
(2)解:直线方程为y=2(x-1),代入y2=4x,可得x2-3x+1=0,
设S(x1,y1),T(x2,y2),则x1+x2=3,∴|ST|=x1+x2+2=5;
(3)证明:设P(x1,y1),Q(x2,y2),
由题意可知y1+y2≠0,y1y2<0.
∵x轴是∠PBQ的角平分线,∴kPB=-kQB,
∴化为4+y1y2=0.
直线PQ的方程为y-y1=$\frac{4}{{y}_{2}+{y}_{1}}$(x-$\frac{{{y}_{1}}^{2}}{4}$),
化为y(y1+y2)+4=4x,令y=0,则x=1,
∴直线PQ过定点(1,0)
点评 本题综合考查了抛物线的定义与标准方程、直线与抛物线相交问题、直线方程及过定点问题、斜率计算公式等基础知识,考查了推理能力、数形结合的思想方法、计算能力、分析问题和解决问题的能力,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
15.直线y=kx+1-2k与椭圆$\frac{x^2}{9}+\frac{y^2}{4}=1$的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 不确定 |
10.一个袋中装有大小相同的5个白球和3个红球,现在不放回的取2次球,每次取出一个球,记“第1次拿出的是白球”为事件A,“第2次拿出的是白球”为事件B,则P(B|A)是( )
| A. | $\frac{5}{8}$ | B. | $\frac{5}{16}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{14}$ |
14.函数f(x)=(m2-m-1)xm是幂函数,且在x∈(0,+∞)上为增函数,则实数m的值是( )
| A. | -1 | B. | 2 | C. | 3 | D. | -1或2 |
15.已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且$\frac{2x+3}{x}>-\frac{{{f^'}(x)}}{f(x)}$总成立,则下列不等式成立的是( )
| A. | e2e+3f(e)<e2ππ3f(π) | B. | e2e+3f(π)>e2ππ3f(e) | C. | e2e+3f(π)<e2ππ3f(e) | D. | e2e+3f(e)>e2ππ3f(π) |