题目内容
7.对于实数a,b,定义运算“?”:a?b=$\left\{\begin{array}{l}{a}^{2}-ab,a≤b\\{b}^{2}-ab,a>b\end{array}\right.$,设f(x)=(2x-1)?(x-1),且关于x的方程f(x)-m=0恰有三个互不相等的实数根,则实数m的取值范围是(0,$\frac{1}{4}$).分析 根据题意确定函数的解析式为f(x)=$\left\{\begin{array}{l}2{x}^{2}-x,x≤0\\ x-{x}^{2},x>0\end{array}\right.$,画出函数的图象从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时m的取值范围.
解答 解:由 2x-1≤x-1 可得 x≤0,由 2x-1>x-1 可得 x>0.
∴根据题意得f(x)=$\left\{\begin{array}{l}(2{x-1)}^{2}-(2x-1)(x-1),x≤0\\({x-1)}^{2}-(2x-1)(x-1),x>0\end{array}\right.$.
即 f(x)=$\left\{\begin{array}{l}2{x}^{2}-x,x≤0\\ x-{x}^{2},x>0\end{array}\right.$,
画出函数的图象,从图象上观察当关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,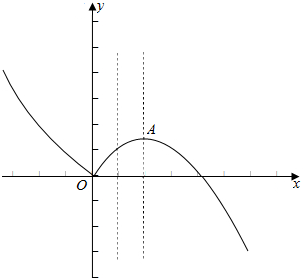
函数的图象和直线y=m有三个不同的交点.
再根据函数的极大值为f($\frac{1}{2}$)=$\frac{1}{4}$,
可得m的取值范围是(0,$\frac{1}{4}$),
故答案为:(0,$\frac{1}{4}$).
点评 本题主要考查函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题

练习册系列答案
相关题目
14.实数x、y,不等式组$\left\{\begin{array}{l}{x≥1且y≤2}\\{y≥kx-3k+2}\end{array}\right.$所确定的可行域内,若目标函数z=y-x仅在点(3,2)取得最小值,则实数k的取值范围是( )
| A. | (0,2) | B. | (1,2) | C. | [0,1) | D. | (0,1) |
15.已知集合A={x|x2≥1},B={x|y=$\sqrt{1-lo{g}_{2}x}$},则A∩B=( )
| A. | (-∞,1]∪(1,2) | B. | (-∞,1]∪(2,+∞) | C. | (0,2] | D. | [1,2] |
12.一个扇形的面积为3π,弧长为2π,则这个扇形中心角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{2π}{3}$ |