Question

已知函数f（x）=

3

sinωx（A＞0，ω＞0）的部分图象如图所示．P、Q分别是图象上的一个最高点和最低点，R为图象与x轴的交点，且四边形OQRP为矩形．
（Ⅰ）求f（x）的解析式；
（Ⅱ）将y=f（x）的图象向右平移

1

2

个单位长度后，得到函数y=g（x）的图象．已知α∈(

3

2

，

5

2

)，g（α）=

3

3

，求f（α）的值．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：计算题,三角函数的图像与性质

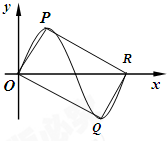
分析：（Ⅰ）设函数f（x）的最小正周期为T，则P（

T

4

，

3

）、Q （

3T

4

，-

3

），由四边形为矩形得

.

OP

•

.

OQ

=

3

16

T²-3=0，故T=4，ω=

π

2

，即可得f（x）=

3

sin

π

2

x．  
（Ⅱ）y=g（x）=f（x-

1

2

）=

3

sin（

π

2

x-

π

4

）可得sin（

π

2

α-

π

4

）=

1

3

，又α∈(

3

2

，

5

2

)，可求得cos（

π

2

α-

π

4

）=-

2 2

3

，从而可求f（α）的值．

解答： 解：（Ⅰ）设函数f（x）的最小正周期为T，则P（

T

4

，

3

）、Q （

3T

4

，-

3

），（2分）
∵四边形OQRP为矩形．∴OP⊥OQ，∴

.

OP

•

.

OQ

=

3

16

T²-3=0，∴T=4．           （5分）
∴ω=

2π

T

=

2π

4

=

π

2

，∴f（x）=

3

sin

π

2

x．                                 （7分）
（Ⅱ）y=g（x）=f（x-

1

2

）=

3

sin（

π

2

x-

π

4

），（8分）
∵g（α）=

3

sin（

π

2

α-

π

4

）=

3

3

，∴sin（

π

2

α-

π

4

）=

1

3

．                          （10分）
又α∈(

3

2

，

5

2

)，∴

π

2

α-

π

4

∈（

π

2

，π），∴cos（

π

2

α-

π

4

）=-

2 2

3

．               （12分）
∴f（α）=

3

sin

π

2

α=

3

sin[（

π

2

α-

π

4

）+

π

4

]=

3

[sin（

π

2

α-

π

4

）cos

π

4

+cos（

π

2

α-

π

4

）sin

π

4

]
=

3

[

1

3

×

2

2

+(-

2 2

3

)×

2

2

]=

6 -4 3

6

．                                  （14分）

点评：本题主要考察了由y=Asin（ωx+φ）的部分图象确定其解析式，函数y=Asin（ωx+φ）的图象变换，属于基本知识的考查．