题目内容

已知非零向量
a
，
b
满足|
a
|=1，且
a
与
a
-
b
的夹角为30°，则|
b
|的取值范围是
 
．
考点：数量积表示两个向量的夹角
专题：平面向量及应用
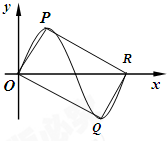
分析：如图所示，设
AB
=
a
，
AC
=
a
-
b
，
CB
=
b
，∠CAB=30°，由图可知，当BC⊥AC时，|
b
|最小，此时|
b
|=
1
2
，从而求得|
b
|的取值范围
解答： 解：如图所示，设
AB
=
a
，
AC
=
a
-
b
，
CB
=
b
，∠CAB=30°，由图可知，当BC⊥AC时，|
b
|最小，
此时|
b
|=
1
2
，所以|b|的取值范围是[
1
2
，+∞)．
故答案为：[
1
2
，+∞）．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
3
sinωx（A＞0，ω＞0）的部分图象如图所示．P、Q分别是图象上的一个最高点和最低点，R为图象与x轴的交点，且四边形OQRP为矩形．
（Ⅰ）求f（x）的解析式；
（Ⅱ）将y=f（x）的图象向右平移
1
2
个单位长度后，得到函数y=g（x）的图象．已知α∈(
3
2
，
5
2
)，g（α）=
3
3
，求f（α）的值．
已知函数f（x）=2sinx（sinx+cosx）
（1）求f（
5π
4
）的值；
（2）求函数f（x）的最小正周期及单调递增区间．
函数y=|x-1|的图象是（　　）
A、
B、
C、
D、
下列函数中值域为R的函数有（　　）
①y=（
1
2
）x    ②y=x2     ③y=
1
x
     ④y=log2x．
A、1个B、2个C、3个D、4个
给出下列关系：①
1
2
=R；②
2
∉Q；③|-3|?N+；④|-
3
|∈Q，其中正确的个数为（　　）
A、1个B、2个C、3个D、4个
已知向量
a
=（sinx，
3
4
），
b
=（cosx，-1）．
（1）当
a
∥
b
时，求cos2x-sin2x的值；
（2）设函数f（x）=2（
a
+
b
）•
b
，且当x∈[0，
π
2
]时，|f（x）-m|≤2恒成立，求m取值范围．
计算：
cos(-45°)cos330°tan585°
tan(-120°)
的值．
已知正四面体OABC的棱长为1．求：（1）
OA
•
OB
；（2）（
OA
+
OB
）•（
CA
+
CB
）（3）|
OA
+
OB
+
OC
|

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网