题目内容
已知等差数列数列 的前
的前 项和为
项和为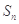 ,等比数列
,等比数列 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: .
.
(Ⅰ)求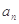 与
与 ;
;
(Ⅱ)设 ,若
,若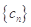 满足:
满足: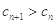 对任意的
对任意的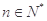 恒成立,求
恒成立,求 的取值范围.
的取值范围.
 的前
的前 项和为
项和为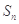 ,等比数列
,等比数列 的各项均为正数,公比是
的各项均为正数,公比是 ,且满足:
,且满足: .
.(Ⅰ)求
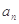 与
与 ;
;(Ⅱ)设
 ,若
,若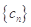 满足:
满足: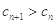 对任意的
对任意的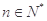 恒成立,求
恒成立,求 的取值范围.
的取值范围.(Ⅰ) ;(Ⅱ)
;(Ⅱ)
 ;(Ⅱ)
;(Ⅱ)
本题考查数列基本量的运算与利用函数单调性解决数列中的恒成立问题。注意处理含参变量的问题的一种重要策略是分离参数。
解:(Ⅰ)由已知可得 ,消去
,消去 得:
得: ,
,
解得 或
或 (舍),
(舍), 从而
从而
(Ⅱ)由(1)知: .
.
∵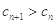 对任意的
对任意的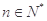 恒成立, 即:
恒成立, 即: 恒成立,
恒成立,
整理得: 对任意的
对任意的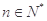 恒成立,·
恒成立,·
即: 对任意的
对任意的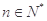 恒成立.
恒成立.
∵ 在区间
在区间  上单调递增,
上单调递增,
 .
.
 的取值范围为
的取值范围为
解:(Ⅰ)由已知可得
 ,消去
,消去 得:
得: ,
,解得
 或
或 (舍),
(舍), 从而
从而
(Ⅱ)由(1)知:
 .
.∵
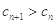 对任意的
对任意的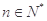 恒成立, 即:
恒成立, 即: 恒成立,
恒成立,整理得:
 对任意的
对任意的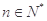 恒成立,·
恒成立,·即:
 对任意的
对任意的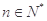 恒成立.
恒成立.∵
 在区间
在区间  上单调递增,
上单调递增,
 .
. 的取值范围为
的取值范围为

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
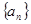 满足a1=0,a2=2,且对任意m,
满足a1=0,a2=2,且对任意m,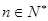 都有
都有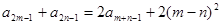
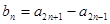
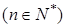 ,证明:
,证明: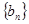 是等差数列;
是等差数列;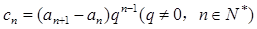 ,求数列
,求数列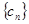 的前n项和Sn。
的前n项和Sn。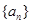 中,
中,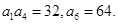
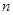 项和为
项和为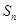 ,求
,求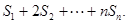
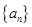 中,
中,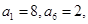 且满足
且满足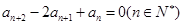 .
.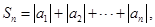 求
求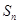 .
.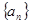 中
中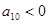 ,
, ,且
,且 ,则在
,则在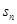 <0中,n的最大值为( )
<0中,n的最大值为( )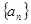 的前
的前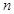 项和为
项和为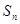 ,已知
,已知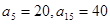 ,
,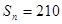 ,求
,求 中,
中, ,其前n项
,其前n项 ,则n=
,则n= 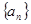 是等差数列,
是等差数列,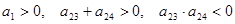 ,则使前
,则使前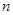 项和
项和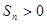 成立的最大正数
成立的最大正数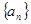 中,
中,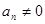 ,且满足
,且满足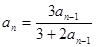
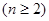 ,则数列
,则数列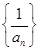 是( )
是( )