题目内容
6．已知sinα=$\frac{1}{3}$，α为第二象限角，则cosα的值为（ ）| A． | $\frac{2}{3}$ | B． | -$\frac{2}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | -$\frac{2\sqrt{2}}{3}$ |
分析 由sinα的值及α为第二象限角，利用同角三角函数间基本关系求出cosα的值即可．
解答 解：∵sinα=$\frac{1}{3}$，且α为第二象限的角，
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{2\sqrt{2}}{3}$．
故选：D．
点评 本题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键，是基础题．
练习册系列答案
相关题目
16．“a=0”是“直线l1：ax+y-1=0与直线l2：x+ay-1=0垂直”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
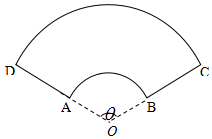某公司拟设计一个扇环形状的花坛（如图所示），该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成．设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f（x）、R米，圆心角为θ（弧度）．
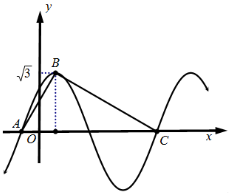已知函数y=$\sqrt{3}$sin（ωx+$\frac{π}{4}$）（ω＞0）．
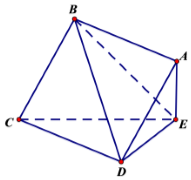如图，边长为2的正方形ABCD所在平面与三角形CDE所在的平面相交于CD，AE⊥平面CDE，且AE=1．