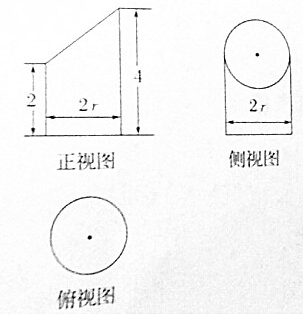
题目内容
15.已知$|{\overrightarrow a}$|=2,$|{\overrightarrow b}|$=$\sqrt{3}$,$\overrightarrow a$•$\overrightarrow b$=3,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 根据向量数量积的计算公式便可由条件求出cos$<\overrightarrow{a},\overrightarrow{b}>$的值,根据向量夹角的范围便可得出向量$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>$=$2\sqrt{3}cos<\overrightarrow{a},\overrightarrow{b}>=3$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\sqrt{3}}{2}$;
又$0≤<\overrightarrow{a},\overrightarrow{b}>≤π$;
∴向量$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{6}$.
故选:D.
点评 考查向量数量积的计算公式,向量夹角的范围,以及已知三角函数值求角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知复数z=1+i(i是虚数单位),则$\frac{4-2i}{z}$的共轭复数是( )
| A. | -1+3i | B. | 1+3i | C. | 1-3i | D. | -1-3i |
5.若某程序框图如图所示,则该程序运行后输出S的值为( )
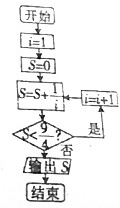

| A. | $\frac{147}{60}$ | B. | $\frac{17}{6}$ | C. | $\frac{25}{4}$ | D. | $\frac{137}{60}$ |