题目内容
某设备的使用年限x与所支出的总维修费用y万元有如下统计资料：
（1）画出散点图，并指出是何种相关？
（2）若用最小二乘法求得
=1.23，求线性回归方程？（精确到0.01）
（3）若要使总维修费用不超过14万元，请你估计大约能使用多少年？（精确到年）
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
（2）若用最小二乘法求得
 |
| b |
（3）若要使总维修费用不超过14万元，请你估计大约能使用多少年？（精确到年）
考点：线性回归方程
专题：计算题,作图题,概率与统计
分析：（1）作散点图，从而指出正相关；
（2）可得
=
=4；
=
=5；再由线性回归方程必过样本的中心点（4，5）求可得线性回归方程；
（3）y=1.23x+0.08≤14解出即可．
（2）可得
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2.2+3.8+5.5+6.5+7.0 |
| 5 |
（3）y=1.23x+0.08≤14解出即可．
解答：
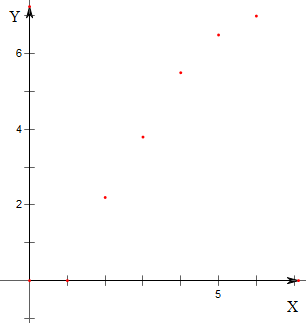解：（1）画出散点图如右图，
维修费用y与使用年限x是正相关；
（2）可得
=
=4；
=
=5；
由线性回归方程必过样本的中心点（4，5）；
∴a=0.08；
线性回归方程为：y=1.23x+0.08；
（3）由y=1.23x+0.08≤14得，
x≤11.3；
又因为x∈N，所以最大x=11；
答：若要使总维修费用不超过14万元，估计大约能使用11年．
解：（1）画出散点图如右图，维修费用y与使用年限x是正相关；
（2）可得
. |
| x |
| 2+3+4+5+6 |
| 5 |
. |
| y |
| 2.2+3.8+5.5+6.5+7.0 |
| 5 |
由线性回归方程必过样本的中心点（4，5）；
∴a=0.08；
线性回归方程为：y=1.23x+0.08；
（3）由y=1.23x+0.08≤14得，
x≤11.3；
又因为x∈N，所以最大x=11；
答：若要使总维修费用不超过14万元，估计大约能使用11年．
点评：本题考查了散点图的作法及线性相关性的应用，属于基础题．
练习册系列答案
相关题目
如图所示，四面体ABCD的四个顶点是长方体的四个顶点（长方体是虚拟图形，起辅助作用），则四面体ABCD的三视图是（用①②③④⑤⑥代表图形）（ ）
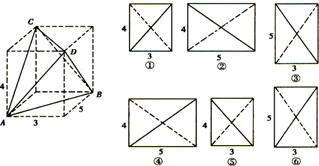
| A、①②⑥ | B、①②③ |
| C、④⑤⑥ | D、③④⑤ |