题目内容
设△ABC的内角A,B,C所对的边长分别为a,b,c,若
=0,则角C= .
|
考点:余弦定理
专题:解三角形
分析:利用余弦定理表示出cosC,将已知等式变形后代入求出cosC的值,即可确定出C的度数.
解答:
解:已知等式变形得:(a+b+c)(a+b-c)-3ab=0,
整理得:(a+b)2-c2-3ab=0,即a2+b2-c2=ab,
∴cosC=
=
,
∵C为三角形内角,
∴C=
,
故答案为:
整理得:(a+b)2-c2-3ab=0,即a2+b2-c2=ab,
∴cosC=
| a2+b2-c2 |
| 2ab |
| 1 |
| 2 |
∵C为三角形内角,
∴C=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:此题考查了余弦定理,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
sin
的值为( )
| 11π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
某学校联欢会安排有小品、相声、朗诵、唱歌、舞蹈五个节目.要求小品播在舞蹈之前,并且这两个节目不能相邻,则节目表不同的排法种数为( )
| A、24 | B、36 | C、72 | D、84 |
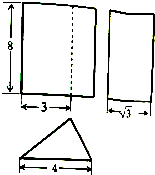 设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于
设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于 定义在区间[-
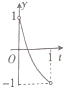
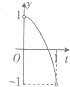
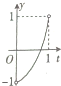
定义在区间[-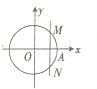 在如图所示的直角坐标系中,点A为圆O:x2+y2=1与x轴的交点,垂直于x轴的动直线l从点A出发,以1m/s的速度沿x轴向左移动,记直线l与圆O的交点为M,N,劣弧MN的长为x,令y=cosx,则y与时间t(0<t<1,单位:s)的函数y=f(x)的图象大致为( )
在如图所示的直角坐标系中,点A为圆O:x2+y2=1与x轴的交点,垂直于x轴的动直线l从点A出发,以1m/s的速度沿x轴向左移动,记直线l与圆O的交点为M,N,劣弧MN的长为x,令y=cosx,则y与时间t(0<t<1,单位:s)的函数y=f(x)的图象大致为( )