题目内容
14. 已知函数f(x)=2sin(2x+$\frac{π}{3}$)
已知函数f(x)=2sin(2x+$\frac{π}{3}$)(1)用五点法画出函数f(x)的大致图象,要有简单列表;
(2)求关于x的不等式f(x)>1的解集.
分析 (1)列表,描点,连线用五点法作函数y=Asin(ωx+φ)的图象即可.
(2)由题意可得sin(2x+$\frac{π}{3}$)>$\frac{1}{2}$,由正弦函数的性质可得2kπ+$\frac{π}{6}$<2x+$\frac{π}{3}$<2kπ+$\frac{5π}{6}$,k∈Z,从而解得关于x的不等式f(x)>1的解集.
解答 解:(1)列表如下:
| 2x+$\frac{π}{3}$ | 0 | $\frac{π}{12}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| y | 0 | 2 | 0 | -2 | 0 |
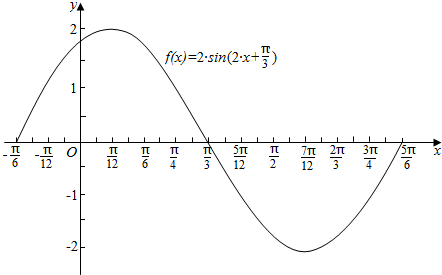
(2)由题意可得:2sin(2x+$\frac{π}{3}$)>1,即sin(2x+$\frac{π}{3}$)>$\frac{1}{2}$,
可得:2kπ+$\frac{π}{6}$<2x+$\frac{π}{3}$<2kπ+$\frac{5π}{6}$,k∈Z,
解得:kπ-$\frac{π}{12}$<x<kπ+$\frac{π}{4}$,k∈Z,
故关于x的不等式f(x)>1的解集为:{x|kπ-$\frac{π}{12}$<x<kπ+$\frac{π}{4}$,k∈Z,}.
点评 本题主要考查了五点法作函数y=Asin(ωx+φ)的图象,考查了正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
4.${∫}_{0}^{1}$|x2-8|dx=( )
| A. | $\frac{21}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{23}{3}$ | D. | $\frac{25}{3}$ |
5.椭圆$\frac{x^2}{m+1}+\frac{y^2}{m}={1^{\;}}({m∈R})$的焦点坐标为( )
| A. | (±1,0) | B. | $({±\sqrt{2m+1},0})$ | C. | (0,±1) | D. | $({0,±\sqrt{2m+1}})$ |
 已知点T(-1,1)在抛物线y2=2px(p>0)的准线上.
已知点T(-1,1)在抛物线y2=2px(p>0)的准线上.