题目内容
17.平行四边形ABCD中,AB=4,AD=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=4,点P在边CD上,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是( )| A. | [-1,8] | B. | [-1,+∞) | C. | [0,8] | D. | [-1,0] |
分析 先根据向量的数量积的运算,求出A=60°,再建立坐标系,得到$\overrightarrow{PA}$•$\overrightarrow{PB}$=x(x-4)+3=x2-4x+3=(x-2)2-1,构造函数f(x),利用函数的单调性求出函数的值域m,问题得以解决.
解答 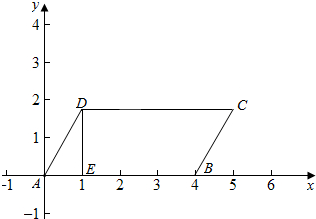 解:∵AB=4,AD=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=4,
解:∵AB=4,AD=2,$\overrightarrow{AB}$•$\overrightarrow{AD}$=4,
∴|$\overrightarrow{AB}$|•|$\overrightarrow{AD}$|cosA=4,
∴cosA=$\frac{1}{2}$,
∴A=60°,
以A为原点,以AB所在的直线为x轴,以AB的垂线为y轴,建立如图所示的坐标系,
∴A(0,0),B(4,0),D(1,$\sqrt{3}$),
设P(x,$\sqrt{3}$),则1≤x≤5,
∴$\overrightarrow{PA}$=(-x,-$\sqrt{3}$),$\overrightarrow{PB}$=(4-x,-$\sqrt{3}$),
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$=x(x-4)+3=x2-4x+3=(x-2)2-1,
设f(x)=(x-2)2-1,
∴f(x)在[1,2)上单调递减,在[2,5]上单调递增,
∴f(x)min=f(2)=-1,f(x)max=f(5)=8,
∴$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是[-1,8],
故选:A.
点评 本题考查了向量的数量积运算和向量的坐标的数量积和函数的最值问题,关键是建立坐标系,属于中档题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
7.下列说法正确的是( )
| A. | 有两个面互相平行,其余各面都是平行四边形的多面体是棱柱 | |
| B. | 过点P(x0,y0)的所有直线的方程都可表示为y-y0=k(x-x0) | |
| C. | 已知点A(x0,y0)是圆C:x2+y2=1内一点,则直线x0x+y0y-1=0与圆C相交 | |
| D. | 圆柱的俯视图可能为矩形 |
12.已知A,B分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P是C上一点,且直线AP,BP的斜率之积为2,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
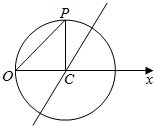 在极坐标系中,已知圆C经过点P($\sqrt{2}$,$\frac{π}{4}$),圆心为直线$ρsin(θ-\frac{π}{3})$=-$\frac{\sqrt{3}}{2}$与极轴的交点,求圆C的直角坐标方程.
在极坐标系中,已知圆C经过点P($\sqrt{2}$,$\frac{π}{4}$),圆心为直线$ρsin(θ-\frac{π}{3})$=-$\frac{\sqrt{3}}{2}$与极轴的交点,求圆C的直角坐标方程.