题目内容
向由平面直角坐标系中的四点(0,0),(1,0),(1,1),(0,1)所围成的平面区域中任意抛掷一粒黄豆,则该黄豆落在曲线y=x3和y=
所围成的平面区域内的概率为( )
| 3 | x |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
考点:几何概型
专题:概率与统计
分析:欲求所投的黄豆落在曲线y=x3和y=
所围成的平面区域内部的概率,须结合定积分计算曲线y=x3和y=
所围成的平面区域的面积,再根据几何概型概率计算公式易求解.
| 3 | x |
| 3 | x |
解答:
解:四点(0,0),(1,0),(1,1),(0,1)所围成的平面区域面积为:1,
曲线y=x3和y=
所围成的平面区域面积为
(
-x3)dx=(
x
-
x4)|
=
,
由几何概型的概率公式得黄豆落在曲线y=x3和y=
所围成的平面区域的概率为
=
;
故选B.
曲线y=x3和y=
| 3 | x |
| ∫ | 1 0 |
| 3 | x |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 4 |
1 0 |
| 1 |
| 2 |
由几何概型的概率公式得黄豆落在曲线y=x3和y=
| 3 | x |
| ||
| 1 |
| 1 |
| 2 |
故选B.
点评:本题考查了几何概型概率的求法;关键是求满足条件的事件的区域面积.

练习册系列答案
相关题目
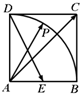 如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量
如图在边长为2的正方形ABCD中,E为边AB的中点,P为以A为圆心、AB为半径的圆弧上的任意一点,设向量