题目内容
9.求以抛物线y2=4x的焦点为圆心,且过坐标原点的圆的标准方程.分析 根据抛物线的性质和圆的标准方程即可求出.
解答 解:抛物线的焦点F(1,0),
因为圆过原点,所以半径R=1
所以所求的圆的标准方程为(x-1)2+y2=1.
点评 本题考查了抛物线的性质和圆的标准方程,属于基础题.

练习册系列答案
相关题目
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的右焦点F,且斜率为2的直线l与双曲线的相交于点A,B,若弦AB的中点横坐标取值范围为(2c,4c),则该双曲线的离心率的取值范围是( )
| A. | (3,4) | B. | (2,3) | C. | $(\sqrt{3},4)$ | D. | $(\sqrt{3},2)$ |
18.过原点的直线l与双曲线$\frac{x^2}{9}-\frac{y^2}{3}=-1$有两个交点,则直线l的倾斜角的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{6}}]$ | B. | $({\frac{π}{6},\frac{5π}{6}})$ | C. | $({\frac{π}{6},\frac{π}{2}})∪({\frac{π}{2},\frac{5π}{6}})$ | D. | $[{\frac{π}{6},\frac{π}{2}})∪({\frac{π}{2},\frac{5π}{6}}]$ |
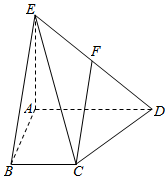 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.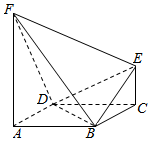 如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.
如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.