题目内容
若点A,B在曲线x2-y2=2(x>0)上,则
•
的最小值为 .
| OA |
| OB |
考点:双曲线的简单性质,平面向量数量积的运算
专题:圆锥曲线中的最值与范围问题
分析:设出A,B的坐标,写出两向量的数量积,把纵坐标用横坐标表示,然后利用基本不等式求得最小值.
解答:
解:设A(x1,y1),B(x2,y2),x1>0,x2>0,且x1x2≥2.
•
=x1x2+y1y2≥x1x2-
•
=x1x2-
≥x1x2-
=x1x2-
=x1x2-|x1x2-2|
=x1x2-(x1x2-2)
=2.
∴
•
的最小值为2.
故答案为:2.
| OA |
| OB |
| x12-2 |
| x22-2 |
=x1x2-
| (x1x2)2-2(x12+x22)+4 |
≥x1x2-
| (x1x2)2-4x1x2+4 |
=x1x2-
| (x1x2-2)2 |
=x1x2-|x1x2-2|
=x1x2-(x1x2-2)
=2.
∴
| OA |
| OB |
故答案为:2.
点评:本题考查了双曲线的简单性质,考查了平面向量的数量积运算,考查了利用基本不等式求最值,体现了数学转化思想方法,是中档题.

练习册系列答案
相关题目
如下图2,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD=
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )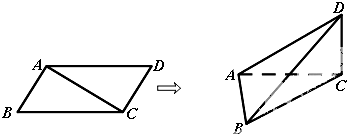
| 5 |

| A、面ABD⊥面BCD |
| B、面ABD⊥面ACD |
| C、面ABC⊥面ACD |
| D、面ABC⊥面BCD |