题目内容
10.已知数列{an}对任意p,q∈N+满足ap+q=ap+aq,且a2=-6,那么a4=-12.分析 利用ap+q=ap+aq,可得a4=a2+2=a2+a2.
解答 解:∵数列{an}对任意p,q∈N+满足ap+q=ap+aq,且a2=-6,
那么a4=a2+2=a2+a2=-12.
故答案为:-12.
点评 本题考查了递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.设α、β、γ是不同的平面,m,n是不同的直线,则由下列条件能得出m⊥β的是( )
| A. | n⊥α,n⊥β,m⊥α | B. | α∩β=m,α⊥β,β⊥γ | C. | m⊥n,n?β | D. | α⊥β,α∩β=n,m⊥n |
2.设复数z1,z2在复平面内的点关于实轴对称,z1=1+i,则$\frac{z_1}{z_2}$=( )
| A. | -i | B. | i | C. | -1 | D. | 1 |
19.用反证法证明命题:“已知x∈R,a=x2-1,b=2x+2,则a,b中至少有一个不小于0”,反设正确的是( )
| A. | 假设a,b都不大于0 | B. | 假设a,b至多有一个大于0 | ||
| C. | 假设a,b都大于0 | D. | 假设a,b都小于0 |
20.有30袋长富牛奶,编号为1至30,若从中抽取6袋进行检验,则用系统抽样确定所抽的编号为( )
| A. | 3,6,9,12,15,18 | B. | 4,8,12,16,20,24 | ||
| C. | 2,7,12,17,22,27 | D. | 6,10,14,18,22,26 |
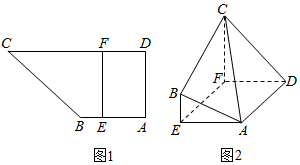 如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.
如图1,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=2,CD=4,点E为线段AB上异于A,B的点,且EF∥AD,沿EF将面EBCF折起,使平面EBCF⊥平面AEFD,如图2.