题目内容

12．设{an}是等差数列，下列结论中正确的是（　　）
A．若a1+a2＜0，则a2+a3＜0
B．若{an}是正数数列，a2+an-1=12，Sn=36．则a3a4的最小值为36
C．若a1＜0，则（a2-a1）（a2-a3）＞0
D．若0＜a1＜a2，则a2$＞\sqrt{{a}_{1}{a}_{3}}$

分析 对于A，举例即可判断，
对于B，根据等差数列的性质和等差数列的前n项和公式，以及基本不等式即可判断，
对于C，根据等差数列的定义即可判断，
对于D，根据等差中项的性质和基本不等式即可判断．

解答 解：对于A，若a1=-2，a2=0，a3=2，满足a1+a2＜0，但a2+a3＞0，故A错误，
对于B，∵{an}是正数数列，a2+an-1=12，
∴a1+an=12，
∵Sn=36，
∴36=$\frac{12n}{2}$，n=6，
∴a1+a6=12，
∴a3+a4=12，
∴a3a4≤（$\frac{{a}_{3}+{a}_{4}}{2}$）2=36，当且仅当a3=a4=6时等号成立，故B错误，
对于C，若a1＜0，设公差为d，则（a2-a1）=d，（a2-a3）=-d，∴（a2-a1）（a2-a3）-d2＜0，故C错误，
对于D，0＜a1＜a2，则2a2=a1+a3＞2$\sqrt{{a}_{1}{a}_{3}}$，∴a2＞$\sqrt{{a}_{1}{a}_{3}}$，故D正确，
故选：D．

点评 本题考查了等差数列的性质以及等差数列的前n项和公式，以及基本不等式，属于中档题．

练习册系列答案
相关题目
2．若f（x）=3-2x，则|f（x+1）+2|≤3的解集为[0，3]．
3．T为常数，定义fT（x）=$\left\{\begin{array}{l}f（x），f（x）≥T\\ T，f（x）＜T\end{array}\right.$，若f（x）=x-lnx，则f3[f2（e）]的值为．（　　）
A．e-lB．eC．3D．e+l
20．定义：[x]（x∈R）表示不超过x的最大整数．例如[1.5]=1，[-0.5]=-1．给出下列结论：
①函数y=[sinx]是周期为2π的周期函数；
②函数y=[sinx]是奇函数；
③函数y=[sinx]的值域是{-1，0，1}；
④函数y=[sinx]-cosx不存在零点．
其中正确命题的序号是①③④（写出所有正确命题的序号）．
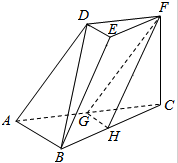7．如图，三棱台DEF-ABC中，底面是以AB为斜边的直角三角形，FC⊥底面ABC，AB=2DE，G，H分别为AC，BC的中点．
（I）求证：直线BD∥平面FGH；
（Ⅱ）若BC=CF=$\frac{AB}{2}$，求二面角A-GH-F的余弦值．
17．已知集合A={x|-3＜x＜2}，B={x|3x＞1}，则A∩（∁RB）=（　　）
A．（-3，1]B．（1，2）C．（-3，0]D．[1，2）
4．设函数f（x）=x3-11x，若对任意m+1＞b＞a＞2m，不等式$\frac{f（b）-f（a）}{b-a}$＜1恒成立，则实数m的取值范围是[-1，1）．
1．已知复数z1=2sinθ-$\sqrt{3}$i，z2=1+（2cosθ）i，i为虚数单位，θ∈[$\frac{π}{3}$，$\frac{π}{2}$]．
（1）若z1•z2为实数，求sec2θ的值；
（2）若复数z1，z2对应的向量分别是$\overrightarrow{a}$，$\overrightarrow{b}$，存在θ使等式（λ$\overrightarrow{a}$-$\overrightarrow{b}$）•（$\overrightarrow{a}$-λ$\overrightarrow{b}$）=0成立，求实数λ的取值范围．
2．有5双不同型号的鞋子
（1）从其中任取4只有多少种不同的取法？
（2）所取的4只中没有2只是同号的取法有多少种？
（3）所取的4只中只有一双是同号的取法又有多少种？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网