题目内容
7.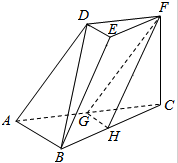 如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.(I)求证:直线BD∥平面FGH;
(Ⅱ)若BC=CF=$\frac{AB}{2}$,求二面角A-GH-F的余弦值.
分析 (I)如图所示,连接DG,CD,设CD∩GF=M,连接MH.由已知可得四边形CFDG是平行四边形,DM=MC.利用三角形的中位线定理可得:MH∥BD,可得BD∥平面FGH;
(Ⅱ)建立空间直角坐标系,求平面的法向量,利用向量法进行求解.
解答 (I)证明:如图所示,连接DG,CD,设CD∩GF=M,连接MH.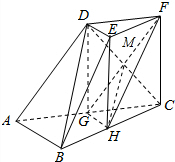
在三棱台DEF-ABC中,AB=2DE,G为AC的中点.
∴$DF\underset{∥}{=}GC$,∴四边形CFDG是平行四边形,
∴DM=MC.又BH=HC,
∴MH∥BD,又BD?平面FGH,MH?平面FGH,
∴BD∥平面FGH;
(Ⅱ)建立以C为坐标原,CA,CB,CF分别为x,y,z轴的空间直角坐标系如图:
设BC=1,则CF=1,AB=2,
则AC=$\sqrt{3}$,
则A($\sqrt{3}$,0,0),C(0,0,0),B(0,1,0),F(0,0,1),
G($\frac{\sqrt{3}}{2}$,0,0),H(0,$\frac{1}{2}$,0),
则AGH的法向量为$\overrightarrow{m}$=(0,0,1),
设GHF的法向量$\overrightarrow{n}$=(x,y,z),
则$\overrightarrow{GH}$=(-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,0),$\overrightarrow{HF}$=(0,$-\frac{1}{2}$,1),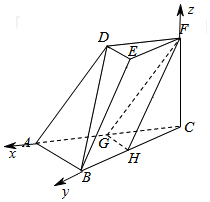
则$\overrightarrow{n}$•$\overrightarrow{GH}$=-$\frac{\sqrt{3}}{2}$x+$\frac{1}{2}$y=0,$\overrightarrow{n}$•$\overrightarrow{HF}$=$-\frac{1}{2}$y+z=0,
令y=2,则x=$\frac{2\sqrt{3}}{3}$,z=1,
即$\overrightarrow{n}$=($\frac{2\sqrt{3}}{3}$,2,1),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{1}{\sqrt{(\frac{2\sqrt{3}}{3})^{2}+{2}^{2}+1}}$=$\frac{\sqrt{57}}{19}$,
∵二面角A-GH-F是钝二面角
∴二面角A-GH-F的余弦为为-$\frac{\sqrt{57}}{19}$.
点评 本题主要考查线面平行的判定,以及二面角的求解,利用二面角的定义作出平面角是解决本题的关键.本题也可以建立坐标系,利用向量法进行求解,综合性较强,运算量较大.

| A. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ | B. | ?m∈[0,1],则$x+\frac{1}{x}≥{2^m}$ | ||
| C. | ?m∈(-∞,0)∪(1,+∞),则$x+\frac{1}{x}≥{2^m}$ | D. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ |
| A. | 若a1+a2<0,则a2+a3<0 | |
| B. | 若{an}是正数数列,a2+an-1=12,Sn=36.则a3a4的最小值为36 | |
| C. | 若a1<0,则(a2-a1)(a2-a3)>0 | |
| D. | 若0<a1<a2,则a2$>\sqrt{{a}_{1}{a}_{3}}$ |