题目内容
2.若f(x)=3-2x,则|f(x+1)+2|≤3的解集为[0,3].分析 求出f(x+1),问题转化为:|2x-3|≤3,解出即可.
解答 解:若f(x)=3-2x,
则|f(x+1)+2|=|3-2(x+1)+2|=|2x-3|≤3,
解得:0≤x≤3,
故不等式的解集为[0,3],
故答案为:[0,3].
点评 本题考查了解绝对值不等式问题,是一道基础题.

练习册系列答案
相关题目
10.定义在R上的函数f(x)满足f(x+2)=f(x),当x∈[0,2)时,f(x)=$\left\{\begin{array}{l}{\frac{1}{2}-2{x}^{2},0≤x<1}\\{-{2}^{1-|x-\frac{3}{2}|},1≤x<2}\end{array}\right.$,函数g(x)=(2x-x2)ex+m,若?x1∈[-4,-2],?x2∈[-1,2],使得不等式f(x1)-g(x2)≥0成立,则实数m的取值范围是( )
| A. | (-∞,-2] | B. | (-∞,$\frac{3}{e}$+2] | C. | [$\frac{3}{e}$+2,+∞) | D. | (-∞,$\frac{3}{e}$-2] |
7.数列{an}前n项和${S_n}={2^n}$,则an=$\left\{{\begin{array}{l}{2,n=1}\\{{2^{n-1}},n≥2}\end{array}}\right.$.
12.设{an}是等差数列,下列结论中正确的是( )
| A. | 若a1+a2<0,则a2+a3<0 | |
| B. | 若{an}是正数数列,a2+an-1=12,Sn=36.则a3a4的最小值为36 | |
| C. | 若a1<0,则(a2-a1)(a2-a3)>0 | |
| D. | 若0<a1<a2,则a2$>\sqrt{{a}_{1}{a}_{3}}$ |
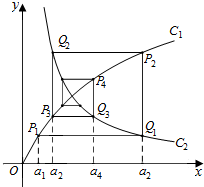 如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}
如图,已知曲线C1:y=$\frac{2x}{x+1}$(x>0)及曲线C2:y=$\frac{1}{3x}$(x>0),C1上的点P1的横坐标为a1(0<a1<$\frac{1}{2}$).从C1上的点Pn(n∈N+)作直线平行于x轴,交曲线C2于点Qn,再从点Qn作直线平行于y轴,交曲线C1于点Pn+1.点Pn(n=1,2,3,…)的横坐标构成数列{an}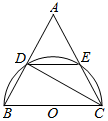 已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.
已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.