题目内容
3.T为常数,定义fT(x)=$\left\{\begin{array}{l}f(x),f(x)≥T\\ T,f(x)<T\end{array}\right.$,若f(x)=x-lnx,则f3[f2(e)]的值为.( )| A. | e-l | B. | e | C. | 3 | D. | e+l |
分析 由条件先求出f(e),根据fT(x)求出f2(e),再求出f3[f2(e)]的值.
解答 解:由题意可得,f(e)=e-lne=e-1<2,
则f2(e)=$\left\{\begin{array}{l}{f(e),f(e)≥2}\\{2,f(e)<2}\end{array}\right.$=2,
又f(2)=2-ln2<2,
所以f3(2)=$\left\{\begin{array}{l}{f(2),f(2)≥3}\\{3,f(2)<3}\end{array}\right.$=3,
即f3[f2(e)]=3,
故选:C.
点评 本题是新定义型的题,解题的关键是理解并会运用新定义,考查分段函数的多层函数值,解题时应根据从内到外的顺序,由分段函数的解析式依次求出函数值,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
18.命题?m∈[0,1],则$x+\frac{1}{x}≥{2^m}$的否定形式是( )
| A. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ | B. | ?m∈[0,1],则$x+\frac{1}{x}≥{2^m}$ | ||
| C. | ?m∈(-∞,0)∪(1,+∞),则$x+\frac{1}{x}≥{2^m}$ | D. | ?m∈[0,1],则$x+\frac{1}{x}<{2^m}$ |
12.设{an}是等差数列,下列结论中正确的是( )
| A. | 若a1+a2<0,则a2+a3<0 | |
| B. | 若{an}是正数数列,a2+an-1=12,Sn=36.则a3a4的最小值为36 | |
| C. | 若a1<0,则(a2-a1)(a2-a3)>0 | |
| D. | 若0<a1<a2,则a2$>\sqrt{{a}_{1}{a}_{3}}$ |
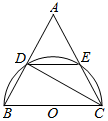 已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.
已知:如图,BC是半圆O的直径,D,E是半圆O上两点,$\widehat{ED}=\widehat{CE}$,CE的延长线与BD的延长线交于点A.